题目内容
(本小题满分14分)过点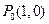 作曲线
作曲线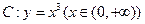 的切线,切点为
的切线,切点为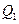 ,过
,过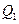 作
作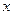 轴的垂线交
轴的垂线交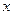 轴于点
轴于点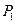 ,又过
,又过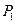 作曲线C的,切点为
作曲线C的,切点为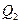 ,过
,过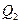 作
作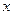 轴的垂线交
轴的垂线交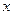 轴于点
轴于点
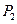 ,…,依次下去得到一系列点
,…,依次下去得到一系列点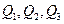 ,…,设点
,…,设点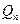 的横坐标为
的横坐标为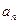 .(1)求数列
.(1)求数列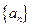 的通项公式;
的通项公式;
(2)求和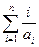
 ;(3)求证:
;(3)求证: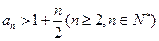 .
.
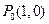 作曲线
作曲线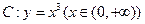 的切线,切点为
的切线,切点为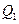 ,过
,过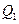 作
作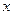 轴的垂线交
轴的垂线交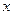 轴于点
轴于点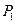 ,又过
,又过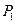 作曲线C的,切点为
作曲线C的,切点为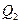 ,过
,过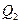 作
作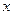 轴的垂线交
轴的垂线交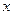 轴于点
轴于点
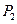 ,…,依次下去得到一系列点
,…,依次下去得到一系列点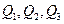 ,…,设点
,…,设点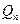 的横坐标为
的横坐标为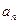 .(1)求数列
.(1)求数列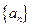 的通项公式;
的通项公式;(2)求和
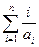
 ;(3)求证:
;(3)求证: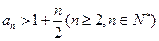 .
.解:(1)∵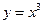 ,∴
,∴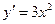 .
.
若切点是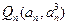 ,
,
则切线方程为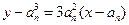 . …………………1分
. …………………1分
当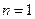 时,切线过点
时,切线过点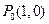 ,
,
即: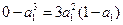 ,
,
依题意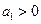 .所以
.所以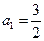 . …………………2分
. …………………2分
当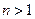 时,切线过点
时,切线过点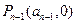 ,
,
即: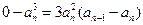 ,
,
依题意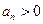 ,所以
,所以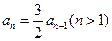 . ………………3分
. ………………3分
所以数列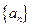 是首项为
是首项为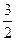 ,
,
公比为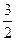 的等比数列.所以
的等比数列.所以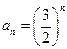 . …………4分
. …………4分
(2)记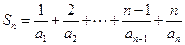 ,
,
因为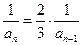 ,
,
所以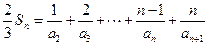 . …………………5分
. …………………5分
两式相减,
得: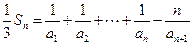

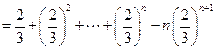
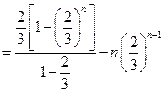
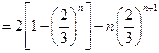 . …………………7分
. …………………7分
∴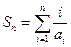

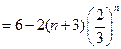 . …………………9分
. …………………9分
(3)证法1: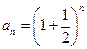

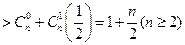 .
.
…………………14分
证法2 :当
:当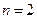 时,
时,
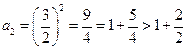 .…………………10分
.…………………10分
假设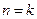 时,结论成立,
时,结论成立,
即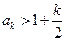 ,
,
则 .
.
即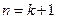 时.
时.
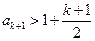 . …………………13分
. …………………13分
综上,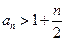
对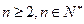 都成立.
都成立.  …………………14分
…………………14分
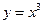 ,∴
,∴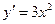 .
.若切点是
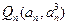 ,
,则切线方程为
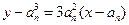 . …………………1分
. …………………1分当
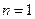 时,切线过点
时,切线过点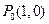 ,
,即:
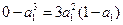 ,
,依题意
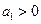 .所以
.所以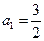 . …………………2分
. …………………2分当
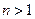 时,切线过点
时,切线过点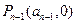 ,
,即:
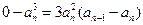 ,
,依题意
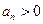 ,所以
,所以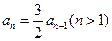 . ………………3分
. ………………3分所以数列
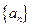 是首项为
是首项为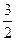 ,
,公比为
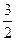 的等比数列.所以
的等比数列.所以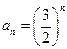 . …………4分
. …………4分(2)记
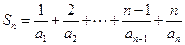 ,
,因为
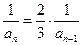 ,
,所以
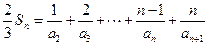 . …………………5分
. …………………5分两式相减,
得:
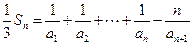

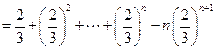
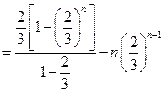
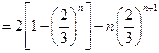 . …………………7分
. …………………7分∴
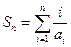

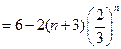 . …………………9分
. …………………9分(3)证法1:
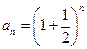

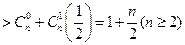 .
. …………………14分
证法2
 :当
:当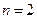 时,
时,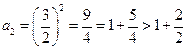 .…………………10分
.…………………10分假设
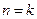 时,结论成立,
时,结论成立,即
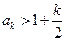 ,
,则
 .
.即
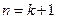 时.
时.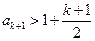 . …………………13分
. …………………13分综上,
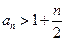
对
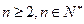 都成立.
都成立.  …………………14分
…………………14分略

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
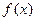 对任意
对任意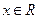 都有
都有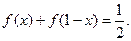
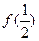 和
和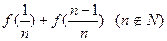 的值;
的值;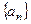 满足:
满足: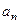 =
=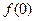 +
+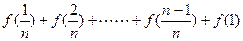 ,数列
,数列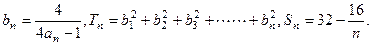
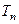 与
与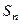 的大小.
的大小.
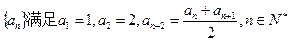
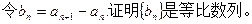
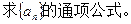
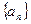
 中,
中,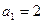 ,
,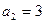 ,
,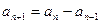 ,
,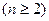 ,设
,设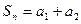
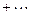
 ,那么
,那么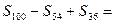 ( )
( )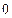
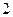
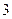
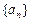 中,
中,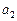 ,
,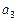 ,
,
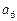 成等比数列,则其公比
成等比数列,则其公比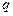 为
为 行.
行.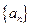 为等差数列,
为等差数列,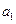 +
+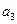 +
+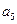 =105,
=105,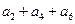 =99,以
=99,以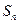 表示
表示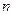 项和,则使得
项和,则使得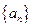 的前
的前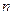 项和为
项和为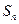 ,若
,若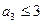 ,
,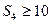 ,则
,则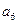 的最大值为 .
的最大值为 .