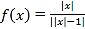题目内容
【题目】已知直线![]() 是双曲线
是双曲线![]() 的一条渐近线,点
的一条渐近线,点![]()
![]() 都在双曲线
都在双曲线![]() 上,直线
上,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,设坐标原点为
,设坐标原点为![]() .
.
(1)求双曲线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(2)设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .问:在
.问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,试求直线
,试求直线![]() 的方程.
的方程.
【答案】(1)![]() ;
;![]() (2)存在定点
(2)存在定点![]() ,其坐标为
,其坐标为![]() 或
或![]() (3)
(3)![]()
【解析】
(1)求得双曲线的渐近线方程,可得![]() ,由题意可得
,由题意可得![]() ,
,![]() ,可得双曲线的方程,求出直线
,可得双曲线的方程,求出直线![]() 的方程,可令
的方程,可令![]() ,求得
,求得![]() 的坐标;(2)求得对称点
的坐标;(2)求得对称点![]() 的坐标,直线
的坐标,直线![]() 方程,令
方程,令![]() ,可得
,可得![]() 的坐标,假设存在
的坐标,假设存在![]() ,运用两直线垂直的条件:斜率之积为
,运用两直线垂直的条件:斜率之积为![]() ,结合
,结合![]() 在双曲线上,化简整理,即可得到定点
在双曲线上,化简整理,即可得到定点![]() ;(3)设出直线
;(3)设出直线![]() 的方程,代入双曲线的方程,运用韦达定理,由向量数量积的性质,可得向量
的方程,代入双曲线的方程,运用韦达定理,由向量数量积的性质,可得向量![]() ,
,![]() 的数量积为0,化简整理,解方程可得
的数量积为0,化简整理,解方程可得![]() 的值,检验判别式大于0成立,进而得到直线
的值,检验判别式大于0成立,进而得到直线![]() 的方程.
的方程.
解:(1)由已知,得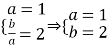 ,故双曲线
,故双曲线![]() 的方程为
的方程为![]()
![]() 为直线AM的一个方向向量,
为直线AM的一个方向向量,
![]() 直线AM的方程为
直线AM的方程为![]() 它与
它与![]() 轴的交点为
轴的交点为![]()
(2)由条件,得![]() 且
且![]() 为直线AN的一个方向向量,
为直线AN的一个方向向量,
故直线AN的方程为![]() 它与
它与![]() 轴的交点为
轴的交点为![]()
假设在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() ,则
,则
由![]()
![]() 及
及![]() 得
得
![]()
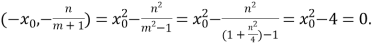
故![]() 即存在定点
即存在定点![]() ,其坐标为
,其坐标为![]() 或
或![]() 满足题设条件.
满足题设条件.
(3)由![]() 知,以
知,以![]() 为邻边的平行四边形的对角线的长相等,故此四边形为矩形,从而
为邻边的平行四边形的对角线的长相等,故此四边形为矩形,从而![]()
由已知,可设直线![]() 的方程为
的方程为![]() 并设
并设![]()
则由![]() 得
得![]()
由![]() 及
及![]() 得
得![]() 且
且![]() (*)
(*)
由![]()
得![]()
故![]() 符合约束条件(*).
符合约束条件(*).
因此,所求直线![]() 的方程为
的方程为![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过![]() 分时,按
分时,按![]() 元/分计费;超过
元/分计费;超过![]() 分时,超出部分按
分时,超出部分按![]() 元/分计费.已知王先生家离上班地点
元/分计费.已知王先生家离上班地点![]() 公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间
公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间 ![]() (分)是一个随机变量.现统计了
(分)是一个随机变量.现统计了![]() 次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间 |
|
|
|
|
频数 |
|
|
|
|
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为![]() 分.(1)写出王先生一次租车费用
分.(1)写出王先生一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分)的函数关系式;(2)若王先生一次开车时间不超过
(分)的函数关系式;(2)若王先生一次开车时间不超过![]() 分为“路段畅通”,设
分为“路段畅通”,设![]() 表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.
表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.