题目内容
【题目】如图,在三棱台![]() 中,二面角
中,二面角![]() 是直二面角,
是直二面角,![]() ,
,![]() ,
,![]() .
.
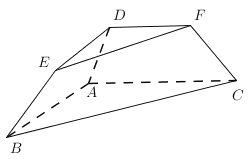
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)由勾股定理可得![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]() 平面
平面![]() ,从而可得
,从而可得![]() ,结合
,结合![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ;(2)在平面
;(2)在平面![]() 内,过点
内,过点![]() 作
作![]() ,由(1)可知
,由(1)可知![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立空间直角坐标系,
轴的正方向,建立空间直角坐标系,![]() 是平面
是平面![]() 的一个法向量,利用向量垂直数量积为零列方程求出平面
的一个法向量,利用向量垂直数量积为零列方程求出平面![]() 的一个法向量,利用空间向量夹角余弦公式可得结果.
的一个法向量,利用空间向量夹角余弦公式可得结果.
详解:(1)连接![]() ,在等腰梯形
,在等腰梯形![]() 中,过
中,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() ,又二面角
,又二面角![]() 是直二面角,
是直二面角,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,又因为
,又因为![]() ,
,![]() ,
,![]() 、
、![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.

(2)如图,在平面![]() 内,过点
内,过点![]() 作
作![]() ,由(1)可知
,由(1)可知![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,设
,设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则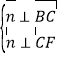 ,所以
,所以![]() ,
,
取![]() ,则
,则![]() ,
,![]() ,
,
即![]() ,
,
由(1)可知![]() 平面
平面![]() ,
,
所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以
![]() ,
,
又二面角![]() 的平面角为锐角,
的平面角为锐角,
所以二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

【题目】近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付,某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),绘制了如图所示的散点图:
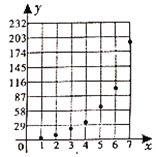
(I)根据散点图判断在推广期内,![]() 与
与![]() (c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(I)的判断结果求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次.
参考数据:
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: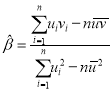 ,
,![]() 。
。
【题目】为了解学生喜欢校内、校外开展活动的情况,某中学一课外活动小组在学校高一年级进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五组,绘制的频率分布直方图如图所示,若将不低于60分的称为
分成五组,绘制的频率分布直方图如图所示,若将不低于60分的称为![]() 类学生,低于60分的称为
类学生,低于60分的称为![]() 类学生.
类学生.

(1)根据已知条件完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为性别与是否为
的前提下认为性别与是否为![]() 类学生有关系?
类学生有关系?
|
| 合计 | |
男 | 110 | ||
女 | 50 | ||
合计 |
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中![]() 类学生的人数为
类学生的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
参考公式:![]() ,其中
,其中![]() .
.
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |