题目内容
【题目】已知f(x)=ax2﹣2(a+1)x+3(a∈R).
(1)若函数f(x)在 ![]() 单调递减,求实数a的取值范围;
单调递减,求实数a的取值范围;
(2)令h(x)= ![]() ,若存在
,若存在 ![]() ,使得|h(x1)﹣h(x2)|≥
,使得|h(x1)﹣h(x2)|≥ ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】
(1)解:①当a=0时,f(x)=﹣2x+3,显然满足;
②  ,③
,③ 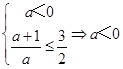 ,
,
综上: ![]()
(2)解:存在 ![]() ,使得|h(x1)﹣h(x2)|≥
,使得|h(x1)﹣h(x2)|≥ ![]() 成立即:
成立即:
在 ![]() 上,h(x)max﹣h(x)min≥
上,h(x)max﹣h(x)min≥ ![]() 成立,
成立,
因为 ![]() ,令
,令 ![]() ,
,
则 ![]() ,
, ![]() .
.
(i)当a≤0时,g(t)在 ![]() 单调递减,所以
单调递减,所以 ![]() ,
,
等价于 ![]() ,所以a≤0.
,所以a≤0.
(ii)当0<a<1时,  ,g(t)在
,g(t)在 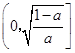 上单调递减,
上单调递减,
在 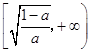 上单调递增.
上单调递增.
①当 ![]() 时,即
时,即 ![]() ,g(t)在
,g(t)在 ![]() 单调递增.
单调递增.
由 ![]() 得到
得到 ![]() ,所以
,所以 ![]() .
.
②当 ![]() 时,
时, ![]() 时,g(t)在
时,g(t)在 ![]() 单调递减,
单调递减,
由 ![]() 得到
得到 ![]() ,所以
,所以 ![]() .
.
③当 ![]() ,即
,即 ![]() 时,
时, 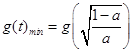 ,
,
最大值则在g(2)与 ![]() 中取较大者,作差比较
中取较大者,作差比较 ![]() ,得到分类讨论标准:
,得到分类讨论标准:
a.当 ![]() 时,
时, ![]() ,此时
,此时 ![]() ,
,
由 ![]() ,
,
得到 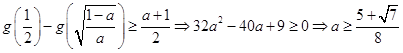 或
或 ![]() ,
,
所以 ![]() .
.
b.当 ![]() 时,
时, ![]() ,此时g(t)max=g(2),
,此时g(t)max=g(2),
由 ![]() ,得到
,得到 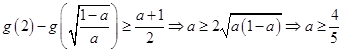 ,
,
所以此时a∈,
在此类讨论中, 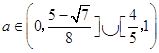 .
.
c.当a≥1时,g(t)在 ![]() 单调递增,由
单调递增,由 ![]() ,
,
得到 ![]() ,所以a≥1,
,所以a≥1,
综合以上三大类情况, 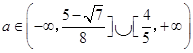
【解析】(1)对a讨论,a=0,a>0,a<0,结合二次函数的图象和单调性的性质,得到不等式组,解不等式即可得到a的范围;(2)由题意可得在 ![]() 上,h(x)max﹣h(x)min≥
上,h(x)max﹣h(x)min≥ ![]() 成立,因为
成立,因为 ![]() ,令
,令 ![]() ,则
,则 ![]() ,
, ![]() .对a讨论,(i)当a≤0时,(ii)当0<a<1时,求出单调性和最值,即可得到a的范围.
.对a讨论,(i)当a≤0时,(ii)当0<a<1时,求出单调性和最值,即可得到a的范围.
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案