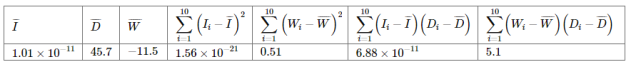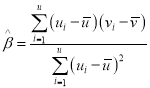题目内容
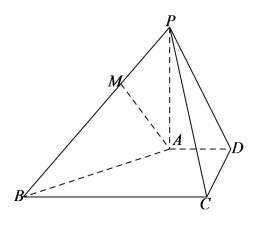
【题目】心理学研究表明,人极易受情绪的影响,某选手参加7局4胜制的兵乒球比赛.
(1)在不受情绪的影响下,该选手每局获胜的概率为![]() ;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到
;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到![]() ;而如果前一局失利的话,此选手该局获胜的概率则降为
;而如果前一局失利的话,此选手该局获胜的概率则降为![]() ,求该选手在前3局获胜局数
,求该选手在前3局获胜局数![]() 的分布列及数学期望;
的分布列及数学期望;
(2)假设选手的三局比赛结果互不影响,且三局比赛获胜的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,求证:
的内角,求证:![]()
【答案】(1)分布列见解析,数学期望1 (2)证明见解析
【解析】
(1)依题意前3局获胜局数![]() 可取
可取![]() ,分别计算概率,列出分布列,即可求出期望.
,分别计算概率,列出分布列,即可求出期望.
(2)根据相互独立事件的概率计算公式可得选手至少胜一局的概率为:![]() 且概率要小于
且概率要小于![]() ,即可得证.
,即可得证.
解:(1)依题意,可知![]() 可取:
可取:![]()
∴![]()
![]()
![]()
![]()
∴随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.
(2)∵![]() span>是锐角三角形,∴
span>是锐角三角形,∴![]() ,则三局比赛中,该选手至少胜一局的概率为:
,则三局比赛中,该选手至少胜一局的概率为:
![]() 由概率的定义可知:
由概率的定义可知:![]() ,故有:
,故有:
![]()

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
【题目】某市食品药品监督管理局开展2020年春季快递餐饮安全检查,对本市的8个快递配餐点进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
快递配餐点编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分 | 82 | 75 | 70 | 66 | 83 | 93 | 95 | 100 |
卫生标准评分 | 81 | 79 | 77 | 75 | 82 | 83 | 84 | 87 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(精确到0.1)
的线性回归方程;(精确到0.1)
(2)现从8个被检查点中任意抽取两个组成一组,若两个点的原料采购加工标准和卫生标准的评分均超过80分,则组成“快递标兵配餐点”,求该组被评为“快递标兵配餐点”的概率.
参考公式: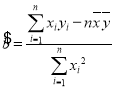 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.