题目内容
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
试题第一问根据题意将问题转化为![]() 在区间
在区间![]() 上的最大值小于等于
上的最大值小于等于![]() 在区间
在区间![]() 上的最大值,之后根据函数的单调性求得相应的最值,第二问转化不等式,将问题转化为一个函数的最小值大于另一个函数的最大值,从而求得结果.
上的最大值,之后根据函数的单调性求得相应的最值,第二问转化不等式,将问题转化为一个函数的最小值大于另一个函数的最大值,从而求得结果.
试题解析:(Ⅰ) 由题意,![]() ,使得不等式
,使得不等式![]() 成立,
成立,
等价于![]() .1分
.1分
![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() 时,
时,![]() 取得最大值1.即
取得最大值1.即![]()
又当![]() 时,
时,![]() ,
,![]()
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
故![]() 在区间
在区间![]() 上单调递减,因此,
上单调递减,因此,![]() 时,
时,![]() .
.
所以![]() ,则
,则![]() .
.
实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)当![]() 时,要证
时,要证![]() ,只要证
,只要证![]() ,
,
即证![]() ,由于
,由于![]() ,
,
只要证![]() .
.
下面证明![]() 时,不等式
时,不等式![]() 成立.
成立.
令![]() ,则
,则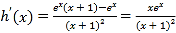 ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以当且仅当![]() 时,
时,![]() 取最小值为1.
取最小值为1.
法一:![]() ,则
,则![]() ,即
,即![]() ,即
,即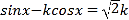 ,
,
由三角函数的有界性,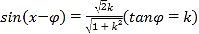 ,即
,即![]() ,所以
,所以![]() ,而
,而![]() ,
,
但当![]() 时,
时,![]() ;
;![]() 时,
时,![]()
所以,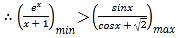 ,即
,即![]()
综上所述,当![]() 时,
时,![]() 成立.
成立.
法二:令![]() ,其可看作点
,其可看作点![]() 与点
与点![]() 连线的斜率
连线的斜率![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() ,
,
由于点![]() 在圆
在圆![]() 上,所以直线
上,所以直线![]() 与圆
与圆![]() 相交或相切,
相交或相切,
当直线![]() 与圆
与圆![]() 相切且切点在第二象限时,
相切且切点在第二象限时,
直线![]() 取得斜率
取得斜率![]() 的最大值为
的最大值为![]() .而当
.而当![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .所以,
.所以,![]() ,即
,即![]()
综上所述,当![]() 时,
时,![]() 成立.
成立.
法三:令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 取得最大值1,而
取得最大值1,而![]() ,
,
但当![]() 时,
时,![]() ;
;![]() 时,
时,![]()
所以,![]() ,即
,即![]()
综上所述,当![]() 时,
时,![]() 成立.
成立.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目