题目内容
19.将2枚质地均匀的骰子抛掷一次,记向上的点数分别为a、b,则事件“a+b=5”的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
分析 将2枚质地均匀的骰子抛掷一次,其基本事件的总个数,由列举法可得事件“a+b=5包含基本事件数目,由古典概型公式,计算可得答案;
解答 解:由题意得,掷骰子1次,其向上的点数有6种情况,
则将一枚骰子连掷两次,基本事件的总个数是6×6=36,即(a,b)的情况有36种,
事件“a+b=8”包含基本事件:(1,4),(2,3),(3,2),(4,1),共4,
∴所求事件的概率$\frac{4}{36}$=$\frac{1}{9}$.
故选:D.
点评 本题考查等可能事件概率计算,涉及一元二次方程有根的充要条件与列举法求基本事件的数目,关键是正确运用列举法,得到基本事件的数目.

练习册系列答案
相关题目
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≤0\\ x+y-8≤0\\ x≥1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
14.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),若a=2b,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | 3 |
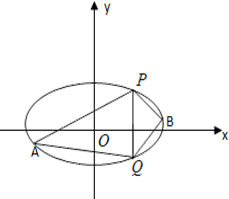 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.