题目内容
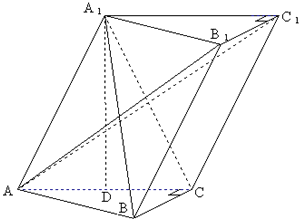 如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.
(1)求证:AC1⊥平面A1BC;
(2)求多面体B1C1ABC的体积.
(1)证明:

A1在底面ABC上的射影在AC上?A1D⊥平面ABC?A1D⊥BC,∵AC⊥BC,
∴BC⊥平面A1C1CA…(3分)AC1?平面A1C1CA,∴BC⊥AC1,BA1⊥AC1,A1B∩BC=B,∴AC1⊥平面A1BC…(7分)
(2)由(1)可知:A1C⊥AC1?ACC1A1是棱形;…(9分)
∵AC=2,点D为中点,AD⊥BC,∴△A1AC为正三角形,∴ …(11分)
…(11分)
∴ …(13分)
…(13分)
分析:(1)由已知,要证AC1⊥平面A1BC,可以证明AC1 与平面A1BC 内两条相交直线BC,BA1 都垂直即可,由A1D⊥平面ABC,证出BC⊥平面A1C1CA,再证出BC⊥AC1即可证明.
(2)多面体B1C1ABC的体积 ,转化求解.
,转化求解.
点评:本题考查线线垂直、线面垂直的定义、性质、判定.空间集合体的体积计算,考查空间想象、论证、计算、转化能力.

A1在底面ABC上的射影在AC上?A1D⊥平面ABC?A1D⊥BC,∵AC⊥BC,
∴BC⊥平面A1C1CA…(3分)AC1?平面A1C1CA,∴BC⊥AC1,BA1⊥AC1,A1B∩BC=B,∴AC1⊥平面A1BC…(7分)
(2)由(1)可知:A1C⊥AC1?ACC1A1是棱形;…(9分)
∵AC=2,点D为中点,AD⊥BC,∴△A1AC为正三角形,∴
 …(11分)
…(11分)∴
 …(13分)
…(13分)分析:(1)由已知,要证AC1⊥平面A1BC,可以证明AC1 与平面A1BC 内两条相交直线BC,BA1 都垂直即可,由A1D⊥平面ABC,证出BC⊥平面A1C1CA,再证出BC⊥AC1即可证明.
(2)多面体B1C1ABC的体积
 ,转化求解.
,转化求解.点评:本题考查线线垂直、线面垂直的定义、性质、判定.空间集合体的体积计算,考查空间想象、论证、计算、转化能力.

练习册系列答案
相关题目
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 (2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且
(2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且 (2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=
(2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=