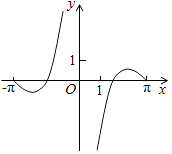题目内容
【题目】已知向量![]() ,函数
,函数![]() ,
,
![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使函数
,使函数![]() ,
,![]() 有四个不同的零点?若存在,求出
有四个不同的零点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在实数m满足条件,且其范围为
;(3)存在实数m满足条件,且其范围为![]() 。
。
【解析】
(1)首先由平面向量数量积的坐标运算求得函数![]() 的解析式,然后求解
的解析式,然后求解![]() 时
时![]() 的值即可;
的值即可;
(2)由题意可得![]() 2cos2x﹣2mcosx,换元后结合二次函数的性质分类讨论求解实数
2cos2x﹣2mcosx,换元后结合二次函数的性质分类讨论求解实数![]() 的值即可;
的值即可;
(3)令![]() 求解
求解![]() 的值,据此求得关于
的值,据此求得关于![]() 的不等式,求解不等式可得实数m的取值范围是
的不等式,求解不等式可得实数m的取值范围是![]() .
.
(1)![]()
![]() =(cos
=(cos![]() ,sin
,sin![]() )(cos
)(cos![]() ,﹣sin
,﹣sin![]() )
)
=cos![]() cos
cos![]() ﹣sin
﹣sin![]() sin
sin![]() =cos(
=cos(![]() +
+![]() )=cos2x,
)=cos2x,
当m=0时,f(x)=![]()
![]() +1=cos2x+1,
+1=cos2x+1,
则f(![]() )=cos(2×
)=cos(2×![]() )+1=cos
)+1=cos![]() +1=
+1=![]() ;
;
(2)∵x∈[﹣![]() ,
,![]() ],
],
∴|![]() +
+![]() |=
|=![]() =
=![]() =2cosx,
=2cosx,
则f(x)=![]()
![]() ﹣m|
﹣m|![]() +
+![]() |+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,
|+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,
令t=cosx,则![]() ≤t≤1, 则y=2t2﹣2mt,对称轴t=
≤t≤1, 则y=2t2﹣2mt,对称轴t=![]() ,
,
①当![]() <
<![]() ,即m<1时,
,即m<1时,
当t=![]() 时,函数取得最小值此时最小值y=
时,函数取得最小值此时最小值y=![]() ﹣m=﹣1,得m=
﹣m=﹣1,得m=![]() (舍),
(舍),
②当![]() ≤
≤![]() ≤1,即m<1时,
≤1,即m<1时,
当t=![]() 时,函数取得最小值此时最小值y=﹣
时,函数取得最小值此时最小值y=﹣![]() =﹣1,得m=
=﹣1,得m=![]() ,
,
③当![]() >1,即m>2时,
>1,即m>2时,
当t=1时,函数取得最小值此时最小值y=2﹣2m=﹣1,得m=![]() (舍),
(舍),
综上若f(x)的最小值为﹣1,则实数![]() .
.
(3)令g(x)=2cos2x﹣2mcosx+![]() m2=0,得cosx=
m2=0,得cosx=![]() 或cosx=
或cosx=![]() ,
,
∴方程cosx=![]() 或
或![]() 在x∈[﹣
在x∈[﹣![]() ,
,![]() ]上有四个不同的实根,
]上有四个不同的实根,
则 ,得
,得 ,则
,则![]() ≤m<
≤m<![]() ,
,
即实数m的取值范围是![]() .
.

【题目】已知直线![]() .
.
(1)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,求
,求![]() 的面积的最小值并求此时直线
的面积的最小值并求此时直线![]() 的方程;
的方程;
(3)已知点![]() ,若点
,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值并求此时直线
的最大值并求此时直线![]() 的方程.
的方程.
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式:  ,
, ![]() .
.
参考数据: ![]() .
.