题目内容
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求实数a,b的值;
(2)判断并证明f(x)在(﹣∞,+∞)上的单调性;
(3)若对任意实数t∈R,不等式f(kt2﹣kt)+f(2﹣kt)<0恒成立,求k的取值范围.
【答案】
(1)解:由于定义域为R的函数f(x)= ![]() 是奇函数,
是奇函数,
则 ![]() 即
即 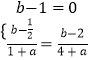 ,解得
,解得 ![]() ,
,
即有f(x)= ![]() ,经检验成立
,经检验成立
(2)解:f(x)在(﹣∞,+∞)上是减函数.
证明:设任意x1<x2,
f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
由于x1<x2,则2x1<2x2,则有f(x1)>f(x2),
故f(x)在(﹣∞,+∞)上是减函数
(3)解:不等式f(kt2﹣kt)+f(2﹣kt)<0,
由奇函数f(x)得到f(﹣x)=﹣f(x),
f(kt2﹣kt)<﹣f(2﹣kt)=f(kt﹣2),
再由f(x)在(﹣∞,+∞)上是减函数,
则kt2﹣kt>kt﹣2,即有kt2﹣2kt+2>0对t∈R恒成立,
∴k=0或 ![]() 即有k=0或0<k<2,
即有k=0或0<k<2,
综上:0≤k<2
【解析】(1)由奇函数的条件可得 ![]() 即可得到a,b;(2)运用单调性的定义,结合指数函数的单调性,即可得证;(3)不等式f(kt2﹣kt)+f(2﹣kt)<0,由奇函数f(x)得到f(﹣x)=﹣f(x),f(kt2﹣kt)<﹣f(2﹣kt)=f(kt﹣2),再由单调性,即可得到kt2﹣2kt+2>0对t∈R恒成立,讨论k=0或k>0,△<0解出即可.
即可得到a,b;(2)运用单调性的定义,结合指数函数的单调性,即可得证;(3)不等式f(kt2﹣kt)+f(2﹣kt)<0,由奇函数f(x)得到f(﹣x)=﹣f(x),f(kt2﹣kt)<﹣f(2﹣kt)=f(kt﹣2),再由单调性,即可得到kt2﹣2kt+2>0对t∈R恒成立,讨论k=0或k>0,△<0解出即可.
【考点精析】根据题目的已知条件,利用奇偶性与单调性的综合的相关知识可以得到问题的答案,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目