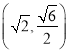题目内容
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆
,以原点为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
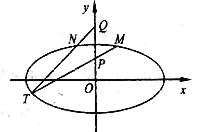
(2)已知点![]() ,设
,设![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的不同两点,直线
轴对称的不同两点,直线![]() 与
与![]() 相交于点
相交于点![]() ,求证:点
,求证:点![]() 在椭圆上.
在椭圆上.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】(1)解:由题意知b=![]() =
=![]() .
.
因为离心率e=![]() =
=![]() ,所以
,所以![]() =
=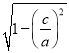 =
=![]() .所以a=2
.所以a=2![]() .
.
所以椭圆C的方程为![]() =1.
=1.
(2)证明:由题意可设M,N的坐标分别为(x0,y0),(-x0,y0),则直线PM的方程为y=![]() x+1,①
x+1,①
直线QN的方程为y=![]() x+2.②
x+2.②
(证法1)联立①②解得x=![]() ,y=
,y=![]() ,即T
,即T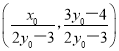 .
.
由![]() =1可得
=1可得![]() =8-4
=8-4![]() .
.
因为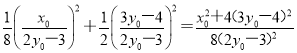
=![]() =1,所以点T坐标满足椭圆C的方程,即点T在椭圆C上.
=1,所以点T坐标满足椭圆C的方程,即点T在椭圆C上.
(证法2)设T(x,y).联立①②解得x0=![]() ,y0=
,y0=![]() .
.
因为![]() =1,所以
=1,所以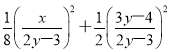 =1.整理得
=1.整理得![]() =(2y-3)2,所以
=(2y-3)2,所以![]() -12y+8=4y2-12y+9,即
-12y+8=4y2-12y+9,即![]() =1.
=1.
所以点T坐标满足椭圆C的方程,即点T在椭圆C上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目