题目内容
13.(文)不等式ax2+bx+2>0的解集为($-\frac{1}{2},\frac{1}{3}$),则ab的值为( )| A. | 24 | B. | -24 | C. | 12 | D. | -12 |
分析 由题意可知,$-\frac{1}{2},\frac{1}{3}$为方程ax2+bx+2=0的两根,利用根与系数的关系列式求出a,b的值,则答案可求.
解答 解:∵不等式ax2+bx+2>0的解集为($-\frac{1}{2},\frac{1}{3}$),
∴可知$-\frac{1}{2},\frac{1}{3}$为方程ax2+bx+2=0的两根,
则$\left\{\begin{array}{l}{-\frac{1}{2}+\frac{1}{3}=-\frac{b}{a}}\\{-\frac{1}{2}×\frac{1}{3}=\frac{2}{a}}\end{array}\right.$,解得:a=-12,b=-2.
∴ab=24.
故选:A.
点评 本题考查一元二次不等式的解法,考查了一元二次方程的根与系数的关系,是基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
5.方程|x|+|y|=1表示的曲线是( )
| A. |  | B. | 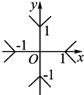 | C. | 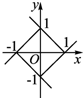 | D. | 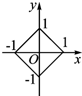 |
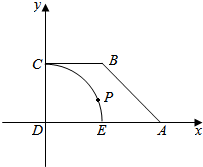 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.