题目内容
18.在直角坐标平面xOy内,一条光线从点(2,4)射出,经直线x+y-1=0反射后,经过点(3,2),则反射光线的方程为x-26y+1=0.分析 设点P点(2,4)关于直线x+y-1=0的对称点为P′(a,b),则$\left\{\begin{array}{l}{\frac{2+a}{2}+\frac{4+b}{2}-1=0}\\{\frac{b-4}{a-2}×(-1)=-1}\end{array}\right.$,解得a,b.再利用点斜式即可得出.
解答 解:设点P点(2,4)关于直线x+y-1=0的对称点为P′(a,b),
则$\left\{\begin{array}{l}{\frac{2+a}{2}+\frac{4+b}{2}-1=0}\\{\frac{b-4}{a-2}×(-1)=-1}\end{array}\right.$,解得a=-3,b=-1.
∴反射光线的斜率为:$\frac{-1-2}{-3-3}$=$\frac{1}{2}$,
∴反射光线的方程y-2=$\frac{1}{2}$(x-3),
化为x-2y+1=0.
故答案为:x-2y+1=0.
点评 本题考查了垂直平分线的性质、中点坐标公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.若点P是抛物线x2=4y上一动点,则点P到直线x-2y-3=0和x轴的距离之和的最小值是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}-1$ |
9.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
(Ⅰ)在答题卡上作出这些数据的频率分布直方图:
(Ⅱ)估计这种产品质量指标值的众数、中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
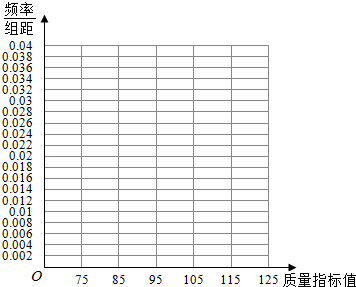
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(Ⅱ)估计这种产品质量指标值的众数、中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?

13.(文)不等式ax2+bx+2>0的解集为($-\frac{1}{2},\frac{1}{3}$),则ab的值为( )
| A. | 24 | B. | -24 | C. | 12 | D. | -12 |