题目内容
已知a,b是不相等的正数,x=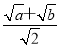 ,y=
,y=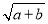 ,则x,y的大小关系是________.
,则x,y的大小关系是________.
x<y
【解析】∵x2= =
=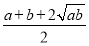 =
= <
<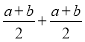 =a+b.=(
=a+b.=(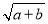 )2=y2,∴x<y.
)2=y2,∴x<y.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
题目内容
已知a,b是不相等的正数,x=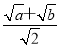 ,y=
,y=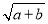 ,则x,y的大小关系是________.
,则x,y的大小关系是________.
x<y
【解析】∵x2= =
=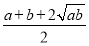 =
= <
<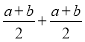 =a+b.=(
=a+b.=(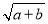 )2=y2,∴x<y.
)2=y2,∴x<y.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案