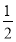Question

平面内有n(n∈N＋，n≥2)条直线，其中任何两条不平行，任何三条不过

同一点，证明：交点的个数f(n)＝.

 

Answer 1

见解析

【解析】(1)当n＝2时，两条直线的交点只有一个，

又f(2)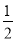＝×2×(2－1)＝1，

∴当n＝2时，命题成立．

(2)假设n＝k，∈N＋，且(k>2)时，命题成立，即平面内满足题设的任何k条直线交点个数f(k)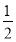＝k(k－1)，

那么，当n＝k＋1时，任取一条直线l，除l以外其他k条直线交点个数为f(k)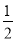＝k(k－1)，l与其他k条直线交点个数为k，从而k＋1条直线共有f(k)＋k个交点，

即f(k＋1)＝f(k)＋k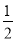＝k(k－1)＋k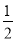＝k(k－1＋2)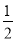＝k(k＋1)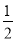＝ (k＋1)[(k＋1)－1]，

这表明，当n＝k＋1时，命题成立．

由(1)、(2)可知，对n∈N＋(n≥2)命题都成立．