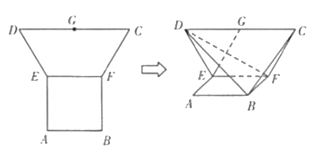
题目内容
【题目】已知数列
，其中
．
（1）若满足
．
①当
，且
时，求
的值；
②若存在互不相等的正整数
，满足
，且
成等差数列，求
的值．
（2）设数列的前
项和为
，数列
的前n项和为
，
，，若，
，且
恒成立，求
的最小值．
【答案】（1）①8②1；（2）5
【解析】
（1）①由递推公式直接计算；②
时数列等差数列，满足题意，
时，利用累加法求出通项
（用
表示），假设存在，由
判断出只有，故此时无解，从而得；
（2）根据
得
的递推关系，注意验证
也满足，再由
得
的递推关系，然后变形为
，从而
时，此式值为5，再计算
时，
，可得
最小值为5．
（1）由
，
，
，累加得
（2）①因
，所以
，
，，当
时，
，满足题意；
当
时，累加得
，所以
若存在
满足条件，化简得
，即
，
此时（舍去）
综上所述，符合条件
的值为1
（2）由
可知
,两式作差可得：
，又由
，可知
故
，所以
对一切的
恒成立
对，两式进行作差可得
,
又由可知
，故
又由
,所以
，
所以当
时
,当
时
,故
的最小值为
新编小学单元自测题系列答案
字词句段篇系列答案【题目】为了调查公司员工的饮食习惯与月收入之间的关系，随机抽取了30名员工，并制作了这30人的月平均收入的频率分布直方图和饮食指数表（说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主）.其中月收入4000元以上员工中有11人饮食指数高于70.
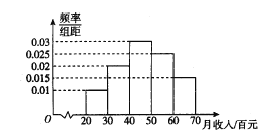
20 | 21 | 21 | 25 | 32 | 33 |
36 | 37 | 42 | 43 | 44 | 45 |
45 | 58 | 58 | 59 | 61 | 66 |
74 | 75 | 76 | 77 | 77 | 78 |
78 | 82 | 83 | 85 | 86 | 90 |
（1）是否有
的把握认为饮食习惯与月收入有关系？若有，请说明理由，若没有，说明理由并分析原因；
（2）从饮食指数在
内的员工中任选2人，求他们的饮食指数均在
内的概率；
（3）经调查某地若干户家庭的年收入
（万元）和年饮支出
（万元）具有线性相关关系，并得到关于的回归直线方程：
.若一个员工的月收入恰好为这30人的月平均收入，估计该人的年饮食支出费用.
附：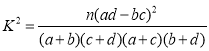
，
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某网店经销某商品，为了解该商品的月销量y（单位：千件）与售价x（单位：元/件）之间的关系，收集5组数据进行了初步处理，得到如下数表：
x | 5 | 6 | 7 | 8 | 9 |
y | 8 | 6 | 4.5 | 3.5 | 3 |
（1）统计学中用相关系数r来衡量两个变量之间线性相关关系的强弱，若
，则认为相关性很强；若
，则认为相关性一般；若
，则认为相关性较弱.请根据上表数据计算y与x之间相关系数r，并说明y与x之间的线性相关关系的强弱（精确到0.01）；
（2）求y关于x的线性回归方程；
（3）根据（2）中的线性回归方程，应将售价x定为多少，可获取最大的月销售金额？（月销售金额＝月销售量×当月售价）
附注：
参考数据：
，
参考公式：相关系数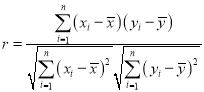
，
线性回归方程
，
，
.
