题目内容
【题目】给定椭圆C:![]() (
(![]() ),称圆心在原点O,半径为
),称圆心在原点O,半径为![]() 的圆是椭圆C的“卫星圆”.若椭圆C的离心率
的圆是椭圆C的“卫星圆”.若椭圆C的离心率![]() ,点
,点![]() 在C上.
在C上.
(1)求椭圆C的方程和其“卫星圆”方程;
(2)点P是椭圆C的“卫星圆”上的一个动点,过点P作直线![]() ,
,![]() 使得
使得![]()
![]()
![]() ,与椭圆C都只有一个交点,且
,与椭圆C都只有一个交点,且![]() ,
,![]() 分别交其“卫星圆”于点M,N,证明:弦长
分别交其“卫星圆”于点M,N,证明:弦长![]() 为定值.
为定值.
【答案】(1)![]() ,
,![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据题意列出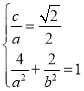 再结合
再结合![]() 即可解出
即可解出![]() ,
,![]() ,从而得到椭圆C的方程和其“卫星圆”方程;
,从而得到椭圆C的方程和其“卫星圆”方程;
(2) 根据![]()
![]()
![]() 分类讨论,当有一条直线斜率不存在时(不妨假设
分类讨论,当有一条直线斜率不存在时(不妨假设![]() 无斜率),可知其方程为
无斜率),可知其方程为![]() 或
或![]() ,这样可求出
,这样可求出![]() ;当两条直线的斜率都存在时,设经过点
;当两条直线的斜率都存在时,设经过点![]() 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为![]() ,与椭圆方程联立,由
,与椭圆方程联立,由![]() 可得
可得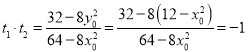 ,所以线段
,所以线段![]() 应为“卫星圆”的直径,即
应为“卫星圆”的直径,即![]() ,故得证.
,故得证.
(1)由条件可得: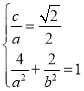
解得![]() ,
,![]()
所以椭圆的方程为![]() ,
,
卫星圆的方程为![]()
(2)①当![]() ,
,![]() 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设![]() 无斜率,
无斜率,
因为![]() 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为![]() 或
或![]() ,
,
当![]() 方程为
方程为![]() 时,此时
时,此时![]() 与“卫星圆”交于点
与“卫星圆”交于点![]() 和
和![]() ,
,
此时经过点![]()
![]() 且与椭圆只有一个公共点的直线是
且与椭圆只有一个公共点的直线是
![]() 或
或![]() ,即
,即![]() 为
为![]() 或
或![]() ,
,
∴![]()
∴线段![]() 应为“卫星圆”的直径,
应为“卫星圆”的直径,
∴![]()
②当![]() ,
,![]() 都有斜率时,设点
都有斜率时,设点![]() ,其中
,其中![]() ,
,
设经过点![]() 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为![]() ,
,
则,
消去y得到![]() ,
,
∴![]()
∴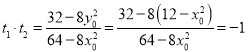
所以![]() ,满足条件的两直线
,满足条件的两直线![]() ,
,![]() 垂直.
垂直.
∴线段![]() 应为“卫星圆”的直径,∴
应为“卫星圆”的直径,∴![]()
综合①②知:因为![]() ,
,![]() 经过点
经过点![]() ,又分别交“卫星圆”于点
,又分别交“卫星圆”于点![]() ,且
,且![]() ,
,![]() 垂直,所以线段
垂直,所以线段![]() 是“卫星圆”
是“卫星圆”![]() 的直径,∴
的直径,∴![]() 为定值.
为定值.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目