Question

【题目】已知圆M：，直线l：，下列四个选项，其中正确的是（ ）

A.对任意实数k与θ，直线l和圆M有公共点

B.存在实数k与θ，直线l和圆M相离

C.对任意实数k，必存在实数θ，使得直线l与圆M相切

D.对任意实数θ，必存在实数k，使得直线l与圆M相切

Answer 1

【答案】AC

【解析】

先确定圆的圆心坐标、直线所过的定点，根据直线与圆的位置关系，结合两点的距离公式、点到直线的距离公式、辅助角公式进行判断即可.

根据题意知圆M的圆心坐标为M（1+cosθ，2+sinθ），半径为1，

，直线l恒过定点N（1，2），

，所以定点N（1，2）在圆M上，

无论θ取何值，都由（1﹣1﹣cosθ）2+（2﹣2﹣sinθ）2＝1，

因此直线l和圆M有公共点，所以选项A正确，选项B错误；

圆心M到直线l的距离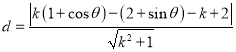

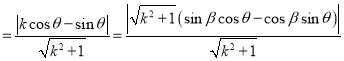
，（其中sinβ，cosβ，tanβ＝k）

当时，，所以对任意实数k，

tanβ＝k，所以必存在实数θ，

使得直线l与圆M相切，所以C正确．

当θ＝0°时，，tanβ不存在，所以D不正确．

故选：AC