题目内容
【题目】已知无穷数列![]() 的各项均为正数,其前
的各项均为正数,其前![]() 项和为
项和为![]() ,
, ![]() .
.
(1)如果![]() ,且对于一切正整数
,且对于一切正整数![]() ,均有
,均有![]() ,求
,求![]() ;
;
(2)如果对于一切正整数![]() ,均有
,均有![]() ,求
,求![]() ;
;
(3)如果对于一切正整数![]() ,均有
,均有![]() ,证明:
,证明: ![]() 能被8整除.
能被8整除.
【答案】(1) ![]() ;(2)
;(2) 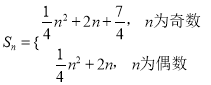 . (3) 见解析.
. (3) 见解析.
【解析】试题分析:(1)由![]() ,得
,得![]() ,根据等比数列的通项公式得到通项;(2)推导出an+1﹣an﹣1=1.a1=4,由anan+1=Sn,得a2=1,a3=5,a4=3,…,由此根据n为偶数和n为奇数,能求出Sn的值;(3)推导出
,根据等比数列的通项公式得到通项;(2)推导出an+1﹣an﹣1=1.a1=4,由anan+1=Sn,得a2=1,a3=5,a4=3,…,由此根据n为偶数和n为奇数,能求出Sn的值;(3)推导出![]() ,分别求出前4项的值,利用数学归纳法能证明a3n﹣1能被8整除.
,分别求出前4项的值,利用数学归纳法能证明a3n﹣1能被8整除.
解析:
(1) 数列![]() 的各项均为正数,由
的各项均为正数,由![]() ,得
,得![]() ,
,
![]() 数列
数列![]() 是等比数列,公比
是等比数列,公比![]() ,从而
,从而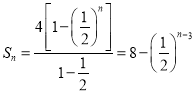
(2) 由![]() 得
得![]() ,两式相减得
,两式相减得![]() ,
,
![]() 此数列各均为正数,
此数列各均为正数, ![]()
![]() ,
, ![]() 数列
数列![]() 和数列
和数列![]() 均是公差为1的等差数列.由
均是公差为1的等差数列.由![]() ,得
,得![]() .
.
当![]() 为偶数时,
为偶数时, ![]()
![]()
当![]() 为奇数时,
为奇数时, ![]()
![]()
 .
.
(3) 由![]() 得
得![]() ,两式相减得
,两式相减得![]() .
.
![]()
![]() ,得
,得![]() ,
, ![]() .
. ![]()
以下证明:对于![]() ,
, ![]() 被8除余数为4,
被8除余数为4, ![]() 被8整除,
被8整除, ![]() 被8除余数为4.
被8除余数为4.
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,命题正确.
,命题正确.
假设![]() 时,命题正确,即
时,命题正确,即![]() ,
, ![]() ,
, ![]() 其中
其中![]() ,
, ![]() .
.
那么, ![]() ,
, ![]()
![]() 为正整数,
为正整数, ![]()
![]() 被8除余数为4.
被8除余数为4.
![]() .
.
![]()
![]() 为正整数,
为正整数, ![]()
![]() 能被8整除.
能被8整除.
![]()
![]() .
. ![]()
![]() 为正整数,
为正整数, ![]()
![]() 被8除余数为4.
被8除余数为4.
即![]() 时,命题也正确.
时,命题也正确.
从而证得,对于一切正整数![]() ,
, ![]() 能被8整除.
能被8整除.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目