Question

【题目】已知数列{an}为正项等比数列，a1＝1，数列{bn}满足b2＝3，a1b1+a2b2+a3b3+…+anbn＝3+（2n﹣3）2n．

（1）求an；

（2）求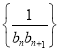的前n项和Tn．

Answer 1

【答案】（1）an＝2n﹣1，n∈N*；（2）

【解析】

本题第（1）题先将代入题干表达式可得，再将代入题干表达式可得，然后设等比数列的公比为，则根据等比数列的定义可得，即可计算出公比的值，即可得到数列的通项公式；

第（2）题由，类比可得，再将两式相减，进一步转化计算，根据第（1）题的结果可计算出数列的通项公式，注意要验证时的情况．然后计算出数列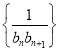的通项公式，再根据通项公式的特点运用裂项相消法可计算出前项和．

解：（1）由题意，当时，，

，，

当时，，

，，，解得，

设等比数列的公比为，则

，

，．

（2）依题意，当时，由，可得

，

两式相减，可得：

，

由（1）知，，

，

当时，也满足上式，

，．

，

．