Question

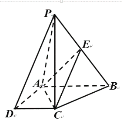
【题目】如图，平面α∩平面β＝l，A，C是α内不同的两点，B，D是β内不同的两点，且A，B，C，D直线l，M，N分别是线段AB，CD的中点．下列判断正确的是（　　）

A.若ABCD，则MNl

B.若M，N重合，则ACl

C.若AB与CD相交，且ACl，则BD可以与l相交

D.若AB与CD是异面直线，则MN不可能与l平行

Answer 1

【答案】BD

【解析】

由若两两相交的平面有三条交线，交线要么相交于一点，要么互相平行判定、、；用反证法证明．

解：若，则、、、四点共面，当时，

平面、、两两相交有三条交线，分别为、、，则三条交线交于一点，

则与平面交于点，与不平行，故错误；

若，两点重合，则，、、、四点共面，

平面、、两两相交有三条交线，分别为、、，

由，得，故正确；

若与相交，确定平面，平面、、两两相交有三条交线，分别为、、，

由，得，故错误；

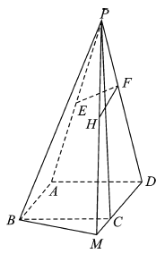
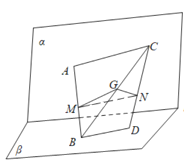
当，是异面直线时，如图，连接，取中点，连接，．

则，，，则，假设，

，，，

又，平面，同理可得，平面，则，与平面平面矛盾．

假设错误，不可能与平行，故正确．

故选：．