题目内容
【题目】已知椭圆![]() 的四个顶点围成的菱形的面积为
的四个顶点围成的菱形的面积为![]() ,椭圆的一个焦点为
,椭圆的一个焦点为![]() .
.
(1)求椭圆的方程;
(2)若![]() ,
,![]() 为椭圆上的两个动点,直线
为椭圆上的两个动点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,当
,当![]() 时,
时,![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
【答案】(1)![]() (2)是,定值
(2)是,定值![]() .
.
【解析】
(1)由题设条件,列出方程组,结合![]() ,求得
,求得![]() 的值,即可求解.
的值,即可求解.
(2)设![]() ,
,![]() ,当直线
,当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() ,联立方程组,结合根与系数的关系和弦长公式,及三角形的面积公式,求得三角形的面积;当直线
,联立方程组,结合根与系数的关系和弦长公式,及三角形的面积公式,求得三角形的面积;当直线![]() 的斜率不存在时,结合椭圆的对称性和三角形的面积公式,即可求解.
的斜率不存在时,结合椭圆的对称性和三角形的面积公式,即可求解.
(1)由椭圆![]() 的四个顶点围成的菱形的面积为
的四个顶点围成的菱形的面积为![]() ,椭圆的一个焦点为
,椭圆的一个焦点为![]() ,
,
可得![]() ,
,![]() ,即
,即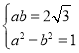 ,解得
,解得![]() ,
,![]() ,
,
故椭圆的方程为![]() .
.
(2)设![]() ,
,![]() ,
,
当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() ,
,
由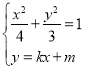 ,消
,消![]() 可得,
可得,![]() ,
,
则![]()
![]() ,即
,即![]() ,
,
且![]() ,
,![]() ,
,
所以![]()

![]() .
.
又由点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]()
![]() .
.
又因为![]() ,
,
所以![]()
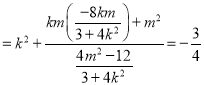 ,
,
化简整理可得![]() ,满足
,满足![]() ,
,
代入![]() ,
,
当直线![]() 的斜率不存在时,由于
的斜率不存在时,由于![]() ,
,
考虑到![]() ,
,![]() 关于
关于![]() 轴对称,不妨设
轴对称,不妨设![]() ,
,![]() ,
,
则点![]() ,
,![]() 的坐标分别为
的坐标分别为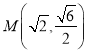 ,
,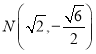 ,
,
此时![]() ,
,
综上可得,![]() 的面积为定值
的面积为定值![]() .
.

【题目】有一片产量很大的水果种植园,在临近成熟时随机摘下某品种水果100个,其质量(均在l至11kg)频数分布表如下(单位: kg):
分组 | | | | | |
频数 | 10 | 15 | 45 | 20 | 10 |
以各组数据的中间值代表这组数据的平均值,将频率视为概率.
(1)由种植经验认为,种植园内的水果质量![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() 近似为样本方差
近似为样本方差![]() .请估算该种植园内水果质量在
.请估算该种植园内水果质量在![]() 内的百分比;
内的百分比;
(2)现在从质量为![]() 的三组水果中用分层抽样方法抽取14个水果,再从这14个水果中随机抽取3个.若水果质量
的三组水果中用分层抽样方法抽取14个水果,再从这14个水果中随机抽取3个.若水果质量![]() 的水果每销售一个所获得的的利润分别为2元,4元,6元,记随机抽取的3个水果总利润为
的水果每销售一个所获得的的利润分别为2元,4元,6元,记随机抽取的3个水果总利润为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]()
![]() ,则
,则![]() .
.
【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.