题目内容
【题目】己知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别是椭圈
分别是椭圈![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 的焦点
的焦点![]() 到双曲线
到双曲线![]() 渐近线的距离为
渐近线的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以线段
两点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,且原点
,且原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用焦点![]() 到双曲线渐近线距离为
到双曲线渐近线距离为![]() 可求得
可求得![]() ;根据离心率可求得
;根据离心率可求得![]() ;由
;由![]() 求得
求得![]() 后即可得到所求方程;(2)由原点到直线
后即可得到所求方程;(2)由原点到直线![]() 距离可得
距离可得![]() ;将直线方程与椭圆方程联立,整理得到韦达定理的形式;根据圆的性质可知
;将直线方程与椭圆方程联立,整理得到韦达定理的形式;根据圆的性质可知![]() ,由向量坐标运算可整理得
,由向量坐标运算可整理得![]() ,从而构造出方程组,结合
,从而构造出方程组,结合![]() 求得结果.
求得结果.
(1)由题意知,![]() ,
,![]()
双曲线方程知,其渐近线方程为:![]()
![]() 焦点
焦点![]() 到双曲线渐近线距离:
到双曲线渐近线距离:![]() ,解得:
,解得:![]()
由椭圆离心率![]() 得:
得:![]()
![]()
![]() 椭圆
椭圆![]() 的方程为:
的方程为:![]()
(2)原点![]() 到直线距离为:
到直线距离为: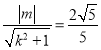 ,整理得:
,整理得:![]()
设![]() ,
,![]()
由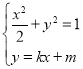 得:
得:![]()
则![]() ,即:
,即:![]()
![]() ,
,![]()
![]() 以
以![]() 为直径的圆过点
为直径的圆过点![]()
![]()
又![]()
![]() ,
,![]()
![]()
![]()
![]()
即:![]()
由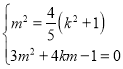 且
且![]() 得:
得: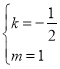 ,满足
,满足![]()
![]() 直线
直线![]() 方程为:
方程为:![]()

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】已知A,B,C三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
A班 | 6 | 6.5 | 7 | |
B班 | 6 | 7 | 8 | |
C班 | 5 | 6 | 7 | 8 |
(1)试估计C班学生人数;
(2)从A班和B班抽出来的学生中各选一名,记A班选出的学生为甲,B班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.