题目内容
【题目】已知椭圆C:![]() 1(a>b>0)的右顶点为A(2,0),离心率为
1(a>b>0)的右顶点为A(2,0),离心率为![]() .
.
(1)求椭圆C的方程;
(2)设过点P(0,﹣2)的直线l与椭圆C相交于M,N两点,当△OMN的面积最大时(O为坐标原点),求直线l的方程.
【答案】(1)![]() 1(2)y
1(2)y![]() x﹣2.
x﹣2.
【解析】
(1)根据椭圆右顶点和离心率,结合![]() ,求得
,求得![]() 的值,由此求得椭圆方程.
的值,由此求得椭圆方程.
(2)设出直线![]() 的方程,联立直线方程和椭圆方程,写出韦达定理,利用弦长公式求得
的方程,联立直线方程和椭圆方程,写出韦达定理,利用弦长公式求得![]() ,利用点到直线的距离公式求得
,利用点到直线的距离公式求得![]() ,由此求得三角形
,由此求得三角形![]() 的面积的表达式,利用换元法,结合基本不等式,求得面积的最大值,以及此时直线
的面积的表达式,利用换元法,结合基本不等式,求得面积的最大值,以及此时直线![]() 的斜率,进而求得直线
的斜率,进而求得直线![]() 的方程.
的方程.
(1)由题意得:a=2,e![]() ,b2=a2﹣c2,解得:a2=2,b2=1,所以椭圆的方程为:
,b2=a2﹣c2,解得:a2=2,b2=1,所以椭圆的方程为:![]() 1;
1;
(2)由题意得直线l的斜率存在且不为零,设直线l的方程:y=kx﹣2,M(x,y),N(x',y'),联立与椭圆的方程整理得:(1+4k2)x2﹣16kx+12=0,△=(16k)2﹣4×12×(1+4k2)>0,得k2![]() ,x+x'
,x+x'![]() ,xx'
,xx'![]() ,所以弦长MN
,所以弦长MN![]() |x﹣x'|
|x﹣x'|![]() 4
4![]() ,原点到直线l的距离d
,原点到直线l的距离d![]() ,所以S△OMN
,所以S△OMN![]() MNd
MNd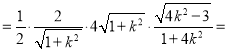
![]() ,令t
,令t![]() (t>0),所以4k2=t2+3, S
(t>0),所以4k2=t2+3, S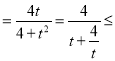 1,当且仅当t=2时等号成立,即k2
1,当且仅当t=2时等号成立,即k2![]() ,满足条件,解得k
,满足条件,解得k![]() ,所以直线l的方程为:y
,所以直线l的方程为:y![]() x﹣2.
x﹣2.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
【题目】已知A,B,C三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
A班 | 6 | 6.5 | 7 | |
B班 | 6 | 7 | 8 | |
C班 | 5 | 6 | 7 | 8 |
(1)试估计C班学生人数;
(2)从A班和B班抽出来的学生中各选一名,记A班选出的学生为甲,B班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.