题目内容
4. 已知四棱柱ABCD-A1B1C1D1的三视图如图所示.
已知四棱柱ABCD-A1B1C1D1的三视图如图所示.(1)画出此四棱柱的直观图,并求出四棱柱的体积;
(2)若E为AA1上一点,EB∥平面A1CD,试确定E点位置,并证明EB⊥平面AB1C1D.
分析 (1)根据三视图画出四棱柱的直观图,由四棱柱的体积$V={S_{ABCD}}•A{A_1}=6\sqrt{2}$即可得解.
(2)作EF∥AD交A1D于F,连CF,则易证BCFE为平行四边形且$AE=\sqrt{2}$.由$\frac{AE}{AB}=\frac{AB}{{B{B_1}}}$,可证BE⊥AB1,又AD⊥AA1,AD⊥AB,AA1∩AB=A.
可证AD⊥平面AA1B1B,BE?平面AA1B1B,从而证明AD⊥BE,即可证明BE⊥平面AB1C1D.
解答 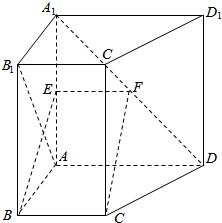 (本小题满分14分)
(本小题满分14分)
解:(1)四棱柱的直观图参考右下图; …(3分)
四棱柱的体积$V={S_{ABCD}}•A{A_1}=6\sqrt{2}$;…(6分)
(2)存在E为AA1的中点,EB∥平面A1CD,并EB⊥平面AB1C1D.
证明:作EF∥AD交A1D于F,连CF,则BCFE共面,
∵EB∥平面A1CD,
∴BE∥CF,又EF∥BC,
∴BCFE为平行四边形.
∴$EF=BC=\frac{1}{2}AD$,
∴E为AA1的中点.…(10分)
在矩形AA1B1B中,AB=2,$AE=\sqrt{2}$.
∴$\frac{AE}{AB}=\frac{AB}{{B{B_1}}}$,
∴△AB1B~△ABE,
∴∠AB1B=∠ABE,
∴BE⊥AB1,又AD⊥AA1,AD⊥AB,AA1∩AB=A.
∴AD⊥平面AA1B1B,BE?平面AA1B1B.
∴AD⊥BE,AB1∩AD=A,
∴BE⊥平面AB1C1D.…(14分)
点评 本小题主要考查空间中线面关系,空间想象能力、逻辑推理能力和运算求解能力,属于中档题.

练习册系列答案
相关题目
14.在如下的2×2列联表中,若分类变量X和Y有关系,比值相差大的应该是( )
| X1 | X2 | 总计 | |
| Y1 | a | b | a+b |
| Y2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| A. | $\frac{a}{a+b}$与$\frac{c}{c+d}$ | B. | $\frac{a}{c+d}$与$\frac{c}{a+b}$ | C. | $\frac{a}{a+d}$与$\frac{c}{b+c}$ | D. | $\frac{a}{b+d}$与$\frac{c}{a+c}$ |
12.已知随机变量X的概率分布列如表所示:且X的数学期望EX=6,则( )
| X | 5 | 6 | 7 | 8 |
| p | 0.4 | a | b | 0.1 |
| A. | a=0.3,b=0.2 | B. | a=0.2,b=0.3 | C. | a=0.4,b=0.1 | D. | a=0.1,b=0.4 |
13.已知sin(α+β)cosβ-cos(α+β)sinβ=$\frac{3}{5}$,且α在第二象限,则tan$\frac{α}{2}$( )
| A. | $\frac{1}{3}$或-3 | B. | 3 | C. | $\frac{1}{3}$ | D. | 3或-$\frac{1}{3}$ |