题目内容
11．化简：（1-x）5+（x+1）5．分析 按照二项式定理把（1-x）5 和（x+1）5 分别展开，可得：（1-x）5+（x+1）5的结果．
解答 解：（1-x）5+（x+1）5 =${C}_{5}^{0}$-${C}_{5}^{1}$•x+${C}_{5}^{2}$•x2-${C}_{5}^{3}$•x3+${C}_{5}^{4}$•x4-${C}_{5}^{5}$•x5+${C}_{5}^{0}$+${C}_{5}^{1}$•x+${C}_{5}^{2}$•x2+${C}_{5}^{3}$•x3+${C}_{5}^{4}$•x4+${C}_{5}^{5}$x5
= 2${C}_{5}^{0}$+2${C}_{5}^{2}$•x2+2${C}_{5}^{4}$•x4=2+20x2+10x4．
点评 本题主要考查二项式定理的应用，二项式展开式的通项公式，属于基础题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
1．如图的框图的功能是计算$\frac{1}{2}+\frac{1}{2^2}+…+\frac{1}{{{2^{10}}}}$的值，那么在①②两处应填入（ ）
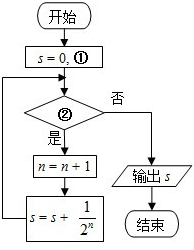
| A． | n=0或和n≤10 | B． | n=1或和n≤10 | C． | n=0或和n＜10 | D． | n=1或和n＜10 |