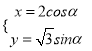题目内容
【题目】若函数f（x）的零点与g（x）=4x+2x﹣2的零点之差的绝对值不超过0.25，则f（x）可以是（ ）
A.f（x）=4x﹣1
B.f（x）=（x﹣1）2
C.f（x）=ex﹣1
D.f（x）=ln（x﹣ 
）
【答案】A
【解析】解：∵g（x）=4x+2x﹣2在R上连续，且g（ 
）= 
+ 
﹣2= ﹣ 
＜0，g（ ）=2+1﹣2=1＞0．
设g（x）=4x+2x﹣2的零点为x0 ， 则 ＜x0＜ ，
0＜x0﹣ ＜ ，∴|x0﹣ |＜ ．
又f（x）=4x﹣1零点为x= ；f（x）=（x﹣1）2零点为x=1；
f（x）=ex﹣1零点为x=0；f（x）=ln（x﹣ ）零点为x= ，
故选A．
【考点精析】关于本题考查的函数的零点，需要了解函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点才能得出正确答案．
练习册系列答案
相关题目
