题目内容
已知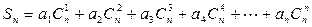 ,
,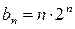
(1)若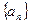 是等差数列,且首项是
是等差数列,且首项是 展开式的常数项的
展开式的常数项的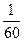 ,公差d为
,公差d为 展开式的各项系数和①求
展开式的各项系数和①求 ②找出
②找出 与
与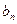 的关系,并说明理由。
的关系,并说明理由。
(2) 若
若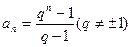 ,且数列
,且数列 满足
满足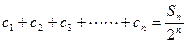 ,求证:
,求证: 是等比数列。
是等比数列。
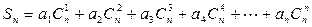 ,
,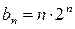
(1)若
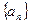 是等差数列,且首项是
是等差数列,且首项是 展开式的常数项的
展开式的常数项的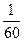 ,公差d为
,公差d为 展开式的各项系数和①求
展开式的各项系数和①求 ②找出
②找出 与
与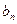 的关系,并说明理由。
的关系,并说明理由。(2)
 若
若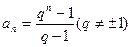 ,且数列
,且数列 满足
满足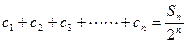 ,求证:
,求证: 是等比数列。
是等比数列。解:(1)设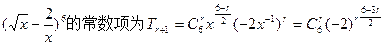
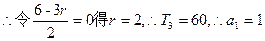 ……………………… 2分
……………………… 2分
又d=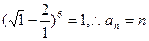 ……………………………………3分
……………………………………3分
① ……………………………………………5分
……………………………………………5分
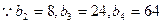 由此可知
由此可知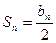 …………………………6分
…………………………6分
下面给出证明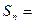
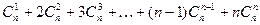 ①
①

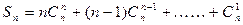 ②
②
①+ ②得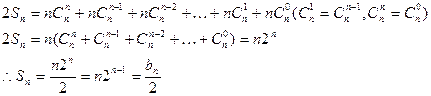 …………8分
…………8分
(2)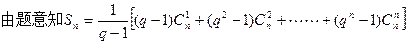
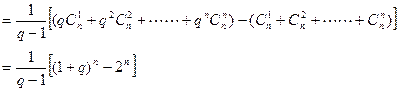 ………………11分
………………11分
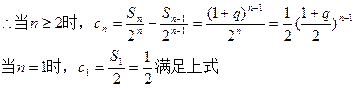 ……………13分
……………13分
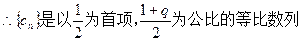 ………………14分
………………14分
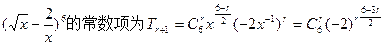
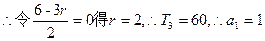 ……………………… 2分
……………………… 2分又d=
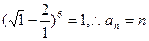 ……………………………………3分
……………………………………3分①
 ……………………………………………5分
……………………………………………5分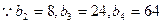 由此可知
由此可知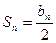 …………………………6分
…………………………6分下面给出证明
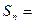
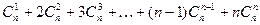 ①
①
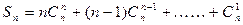 ②
②①+ ②得
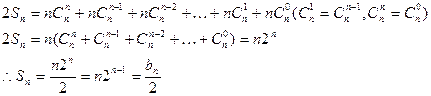 …………8分
…………8分 (2)
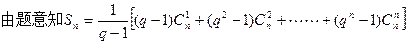
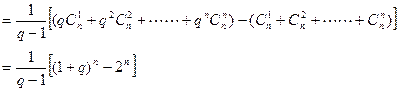 ………………11分
………………11分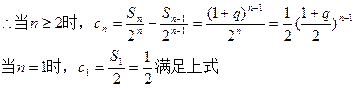 ……………13分
……………13分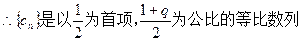 ………………14分
………………14分略

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
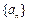 的公差为负数,且
的公差为负数,且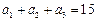 ,若
,若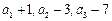 经重新排列后依次可成等比数列,求⑴数列
经重新排列后依次可成等比数列,求⑴数列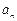 ;⑵数列
;⑵数列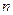 项和
项和 的最大值。
的最大值。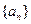 满足
满足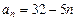 ,
,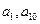 ;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和
;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和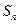 。
。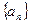 的前
的前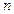 项和为
项和为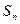 ,对任意
,对任意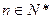 ,点
,点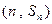 都在函数
都在函数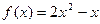 的图像上.
的图像上.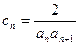 ,
,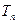 是数列
是数列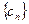 的前
的前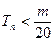 对所有
对所有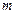 .
.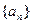 中,d=2,n=15,
中,d=2,n=15,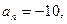 求
求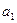
 及
及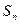
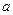 ,
,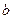 都是正数,并且
都是正数,并且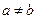 ,求证:
,求证: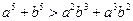
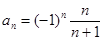 ,则
,则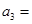 ( )
( )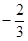
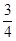
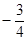
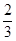
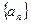 中,
中,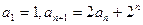
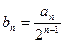 ,证明:数列
,证明:数列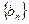 是等差数列;
是等差数列;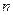 项和
项和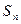 .
.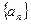 中,若
中,若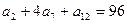 ,则
,则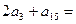 ( )
( )