题目内容
已知数列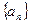 的前
的前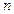 项和为
项和为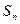 ,对任意
,对任意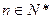 ,点
,点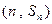 都在函数
都在函数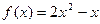 的图像上.
的图像上.
(1)求数列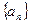 的通项公式;
的通项公式;
(2)设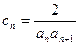 ,
,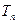 是数列
是数列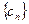 的前
的前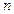 项和,求使得
项和,求使得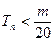 对所有
对所有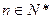 都成立的最小正整数
都成立的最小正整数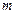 .
.
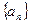 的前
的前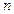 项和为
项和为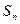 ,对任意
,对任意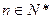 ,点
,点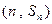 都在函数
都在函数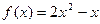 的图像上.
的图像上.(1)求数列
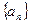 的通项公式;
的通项公式;(2)设
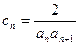 ,
,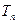 是数列
是数列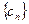 的前
的前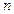 项和,求使得
项和,求使得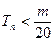 对所有
对所有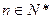 都成立的最小正整数
都成立的最小正整数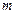 .
.解:(1)由已知,对所有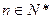 ,
,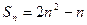 ,
,
当 时,
时,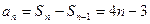 ----------------------------------2分
----------------------------------2分
当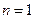 时,
时,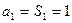 ,
,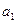 也满足上式-------------------------------3分
也满足上式-------------------------------3分
所以数列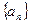 的通项公式为
的通项公式为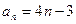 (
(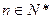 ).------------------4分
).------------------4分
(3)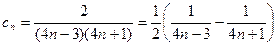 ,----------------------6分,
,----------------------6分,
所以
 9分
9分
由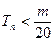 ,得
,得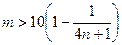 ,因为
,因为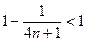 ,所以
,所以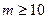
所以,所求的最小正整数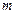 的值为
的值为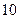 .----------------------------12分
.----------------------------12分
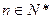 ,
,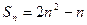 ,
,当
 时,
时,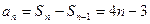 ----------------------------------2分
----------------------------------2分当
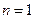 时,
时,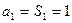 ,
,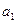 也满足上式-------------------------------3分
也满足上式-------------------------------3分所以数列
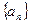 的通项公式为
的通项公式为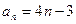 (
(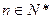 ).------------------4分
).------------------4分(3)
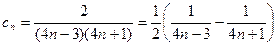 ,----------------------6分,
,----------------------6分,所以
 9分
9分由
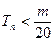 ,得
,得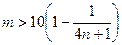 ,因为
,因为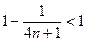 ,所以
,所以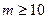
所以,所求的最小正整数
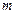 的值为
的值为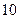 .----------------------------12分
.----------------------------12分略

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
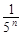 和bn=
和bn=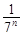 (n∈N*),它们的前n项和依次为An和Bn,则
(n∈N*),它们的前n项和依次为An和Bn,则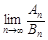 =
=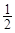
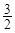
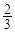
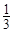
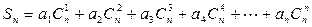 ,
,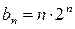
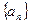 是等差数列,且首项是
是等差数列,且首项是 展开式的常数项的
展开式的常数项的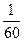 ,公差d为
,公差d为 ②找出
②找出 与
与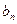 的关系,并说明理由。
的关系,并说明理由。 若
若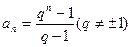 ,且数列
,且数列 满足
满足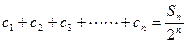 ,求证:
,求证: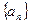 的前n项和为
的前n项和为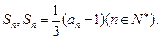
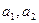 ;
;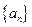 的前
的前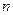 项和
项和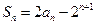 .
.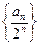 是等差数列;
是等差数列;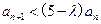 恒成立,求
恒成立,求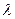 的取值范围.
的取值范围. 值;
值;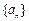 满足:
满足: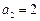 ,
,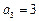 ,
,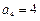 ,
,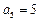 ,且当n≥5时,
,且当n≥5时,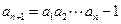 ,若数列
,若数列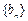 满足对任意
满足对任意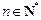 ,有
,有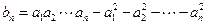 ,则b5= ;当n≥5时,
,则b5= ;当n≥5时,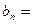
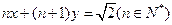 与两坐标轴
与两坐标轴 围成的三角
围成的三角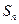
 ,则
,则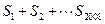 的值为( )
的值为( )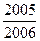
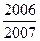
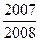
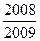
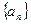 中,
中,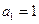 ,且对于任意正整数n,都有
,且对于任意正整数n,都有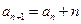 ,则
,则
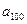 = _______;
= _______;