题目内容
)已知数列{an}的前n项和为Sn,an=5Sn-3(n∈N),求证:数列{an}是等比数列。
解:解:a1=S1,an=Sn-Sn-1(n≥2).又已知an=5Sn-3,∴an-1=5Sn-1-3(n≥2).两式相减,得an-an-1=5(Sn-Sn-1)=5an(n≥2).∴an=-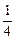 an-1(n≥2).由a1=5S1-3及a1=S1,得a1=
an-1(n≥2).由a1=5S1-3及a1=S1,得a1=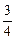 .可见{an}是首项为
.可见{an}是首项为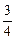 ,公比q=-
,公比q=-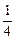 的等比数列.
的等比数列.
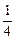 an-1(n≥2).由a1=5S1-3及a1=S1,得a1=
an-1(n≥2).由a1=5S1-3及a1=S1,得a1=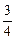 .可见{an}是首项为
.可见{an}是首项为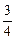 ,公比q=-
,公比q=-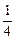 的等比数列.
的等比数列.略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
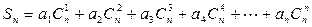 ,
,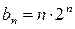
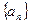 是等差数列,且首项是
是等差数列,且首项是 展开式的常数项的
展开式的常数项的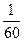 ,公差d为
,公差d为 ②找出
②找出 与
与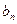 的关系,并说明理由。
的关系,并说明理由。 若
若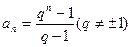 ,且数列
,且数列 满足
满足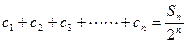 ,求证:
,求证: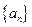 的前
的前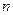 项和
项和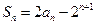 .
.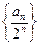 是等差数列;
是等差数列;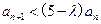 恒成立,求
恒成立,求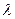 的取值范围.
的取值范围.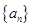 中,已知
中,已知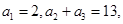
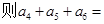 ( )
( ) . 类比上述性质,在等比数列
. 类比上述性质,在等比数列 中,___________________.
中,___________________. 值;
值;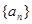 中,
中,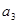 =" 2" ,则该数列的前5项的和为 ( )
=" 2" ,则该数列的前5项的和为 ( ) 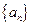 满足
满足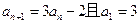 ,
,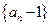 是等比数列;
是等比数列;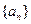 的前
的前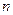 项和为
项和为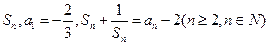
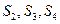 的值;
的值;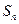 的表达式;并用数学归纳法加以证明。
的表达式;并用数学归纳法加以证明。