题目内容
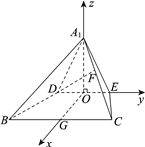
【题目】如图1,在△![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

图1 图2
【答案】(Ⅰ)见解析.(Ⅱ)![]() .(Ⅲ)
.(Ⅲ)![]() .
.
【解析】试题分析:第一问根据等腰三角形的特征,可以得出![]() ,再结合面面垂直的性质定理,可以得出
,再结合面面垂直的性质定理,可以得出![]() 平面
平面![]() ,再根据线面垂直的性质,可以得出以
,再根据线面垂直的性质,可以得出以 ![]() ,之后根据面面垂直的性质和线面垂直的性质得出结果;第二问根据题中的条件,建立空间直角坐标系,利用空间向量求得结果;第三问关于是否存在类问题,都是假设其存在,结合向量所成角的余弦值求得结果.
,之后根据面面垂直的性质和线面垂直的性质得出结果;第二问根据题中的条件,建立空间直角坐标系,利用空间向量求得结果;第三问关于是否存在类问题,都是假设其存在,结合向量所成角的余弦值求得结果.
(Ⅰ)因为在△![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
所以 ![]() ,
,![]() .
.
所以![]() ,又
,又![]() 为
为![]() 的中点,
的中点,
所以 ![]() .
.
因为平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以 ![]() 平面
平面![]() ,
,
所以 ![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,所以
,所以![]() .
.
由(Ⅰ)得![]() ,
,![]() .
.
如图建立空间直角坐标系![]() .
.
由题意得,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则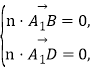 即
即![]()
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() .
.
设直线![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,
,
则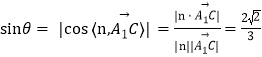 .
.
所以 直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)线段![]() 上存在点
上存在点![]() 适合题意.
适合题意.
设![]() ,其中
,其中![]() .[10分]
.[10分]
设![]() ,则有
,则有![]() ,
,
所以![]() ,从而
,从而![]() ,
,
所以![]() ,又
,又![]() ,
,
所以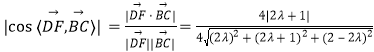 .
.
令![]() ,
,
整理得![]() .
.
解得![]() ,舍去
,舍去![]() .
.
所以 线段![]() 上存在点
上存在点![]() 适合题意,且
适合题意,且![]() .
.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
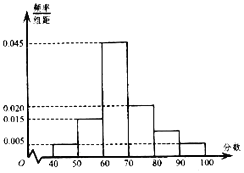
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+![]() )(A>0,ω>0,|
)(A>0,ω>0,|![]() |<
|<![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+ | 0 | 5 | -5 | 0 |
(1)请将上表数据补充完整,并求出函数f(x)的解析式;
(2)将y=f(x)的图象向左平移![]() 个单位,得到函数y=g(x)的图象.若关于x的方程g(x)-m=0在区间[0,
个单位,得到函数y=g(x)的图象.若关于x的方程g(x)-m=0在区间[0,![]() ]上有两个不同的解,求实数m的取值范围.
]上有两个不同的解,求实数m的取值范围.