Question

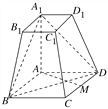
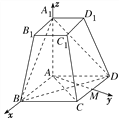
【题目】如图所示，在四棱台ABCDA1B1C1D1中，AA1⊥底面ABCD，四边形ABCD为菱形，∠BAD＝120°，AB＝AA1＝2A1B1＝2.

(1)若M为CD中点，求证：AM⊥平面AA1B1B；

(2)求直线DD1与平面A1BD所成角的正弦值．

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（1）推导出AM⊥CD，由CD∥AB得，AM⊥AB，又AM⊥AA1，由此能证明AM⊥平面AA1B1B

（2）分别以AB，AM，AA1为x轴、y轴、z轴，建立如图所示的空间直角坐标系A﹣xyz，利用向量法能求出直线DD1与平面A1BD所成角θ的正弦值．

试题解析：

(1)证明：连接AC，

∵四边形ABCD为菱形，

∠BAD＝120°，

∴△ACD为等边三角形，

又M为CD中点，

∴AM⊥CD，由CD∥AB得，

AM⊥AB.

∵AA1⊥底面ABCD，AM平面ABCD，∴AM⊥AA1.

又AB∩AA1＝A，

∴AM⊥平面AA1B1B.

(2)∵四边形ABCD为菱形，∠BAD＝120°，AB＝AA1＝2A1B1＝2，

∴DM＝1，AM＝，

∴∠AMD＝∠BAM＝90°，

又AA1⊥底面ABCD，

∴以A为坐标原点，AB，AM，AA1所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系Axyz，

则A1(0,0,2)，B(2,0,0)，D(－1，，0)，D1，

∴＝，＝(－3，，0)，＝(2,0，－2)．

设平面A1BD的法向量为n＝(x，y，z)，

则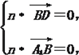即

令x＝1，则n＝(1，，1)，

∴|cos〈n，〉|＝＝＝.

∴/span>直线DD1与平面A1BD所成角的正弦值为.