Question

【题目】(本小题满分12分)已知函数在其定义域内有两个不同的极值点.

（1）求实数的取值范围；

（2）设两个极值点分别为，证明：.

Answer 1

【答案】(1)；(2)证明见解析.

【解析】

试题分析：(1)因为函数在定义域内有两个不同的极值点,所以导函数等于的方程有两个不等的实根,再通过分离转化为两个基本函数有两个不同的交点,函数与直线相切时为临界值；(2)因为是两个极值点,代入方程,由参变分离,可以把用来表示.要证,即证,即,把用换掉,变量集中构造新函数求导判断单调性求出最值.

试题解析：解：（1）依题意，函数的定义域为，∴方程在上有两个不同根，

即方程在上有两个不同根.

转化为函数与函数的图象在上有两个不同交点，如图，

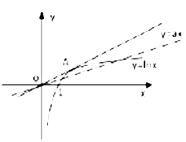
可见，若令过原点且切于函数图象的直线斜率为，只需.

令切点，∴，

又，∴，解得，

于是，∴.

（2）由（1）可知分别是方程的两根，即，，

设，作差得，即.

原不等式等价于

令，则，，

设，，，

∴函数在上单调递增，∴，即不等式成立，

故所证不等式成立.