题目内容
(本题满分16分)已知函数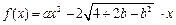 ,
,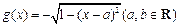 .
.
(1)当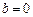 时,若
时,若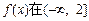 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对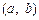 :存在
:存在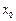 ,使得
,使得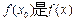 的最大值,
的最大值,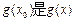 的最小值;
的最小值;
(3)对满足(2)中的条件的整数对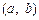 ,试构造一个定义在
,试构造一个定义在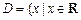 且
且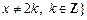 上的函数
上的函数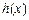 :使
:使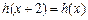 ,且当
,且当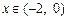 时,
时,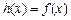 .
.
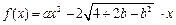 ,
,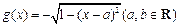 .
.(1)当
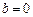 时,若
时,若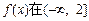 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;(2)求满足下列条件的所有整数对
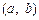 :存在
:存在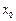 ,使得
,使得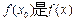 的最大值,
的最大值,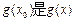 的最小值;
的最小值;(3)对满足(2)中的条件的整数对
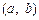 ,试构造一个定义在
,试构造一个定义在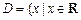 且
且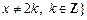 上的函数
上的函数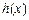 :使
:使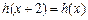 ,且当
,且当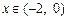 时,
时,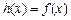 .
.(1)a的取值范围是
(2)满足条件的整数对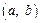 是
是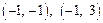
(3)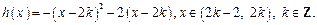

(2)满足条件的整数对
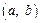 是
是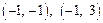
(3)
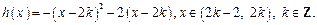
(1)当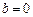 时,
时,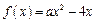 ,………………………………………………1分
,………………………………………………1分
若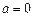 ,
,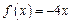 ,则
,则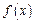 在
在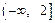 上单调递减,符合题意;………3分
上单调递减,符合题意;………3分
若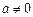 ,要使
,要使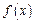 在
在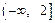 上单调递减,
上单调递减,
必须满足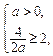 ……………………………………………………………………5分
……………………………………………………………………5分
∴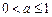 .综上所述,a的取值范围是
.综上所述,a的取值范围是 …………………………………6分
…………………………………6分
(2)若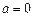 ,
,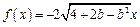 ,则
,则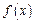 无最大值,………………………7分
无最大值,………………………7分
故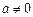 ,∴
,∴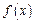 为二次函数,
为二次函数,
要使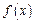 有最大值,必须满足
有最大值,必须满足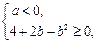 即
即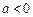 且
且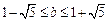 ,…8分
,…8分
此时,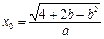 时,
时,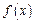 有最大值.………………………………………分
有最大值.………………………………………分
又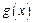 取最小值时,
取最小值时,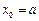 ,………………………………………………………分
,………………………………………………………分
依题意,有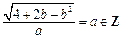 ,则
,则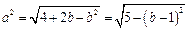 ,…………分
,…………分
∵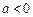 且
且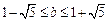 ,∴
,∴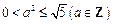 ,得
,得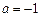 ,………………分
,………………分
此时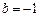 或
或 .
.
∴满足条件的整数对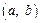 是
是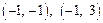 .……………………………12分
.……………………………12分
(3)当整数对是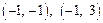 时,
时,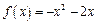
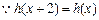 ,
,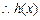 是以2为周期的周期函数,………………………分
是以2为周期的周期函数,………………………分
又当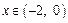 时,,构造
时,,构造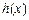 如下:当
如下:当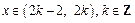 ,则,
,则,
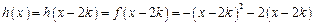 ,
,
故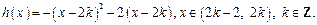 …
…
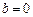 时,
时,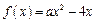 ,………………………………………………1分
,………………………………………………1分若
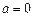 ,
,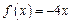 ,则
,则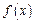 在
在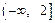 上单调递减,符合题意;………3分
上单调递减,符合题意;………3分若
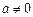 ,要使
,要使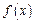 在
在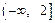 上单调递减,
上单调递减,必须满足
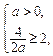 ……………………………………………………………………5分
……………………………………………………………………5分∴
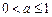 .综上所述,a的取值范围是
.综上所述,a的取值范围是 …………………………………6分
…………………………………6分(2)若
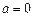 ,
,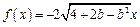 ,则
,则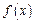 无最大值,………………………7分
无最大值,………………………7分故
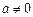 ,∴
,∴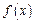 为二次函数,
为二次函数,要使
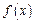 有最大值,必须满足
有最大值,必须满足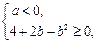 即
即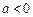 且
且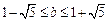 ,…8分
,…8分此时,
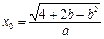 时,
时,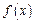 有最大值.………………………………………分
有最大值.………………………………………分又
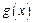 取最小值时,
取最小值时,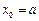 ,………………………………………………………分
,………………………………………………………分依题意,有
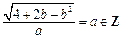 ,则
,则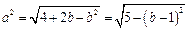 ,…………分
,…………分∵
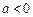 且
且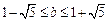 ,∴
,∴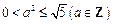 ,得
,得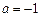 ,………………分
,………………分此时
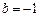 或
或 .
.∴满足条件的整数对
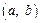 是
是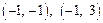 .……………………………12分
.……………………………12分(3)当整数对是
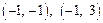 时,
时,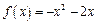
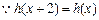 ,
,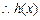 是以2为周期的周期函数,………………………分
是以2为周期的周期函数,………………………分又当
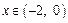 时,,构造
时,,构造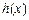 如下:当
如下:当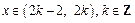 ,则,
,则,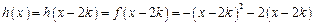 ,
,故
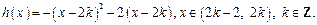 …
…
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
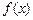 满足
满足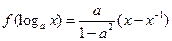 ,其中
,其中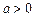 且
且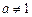 .
.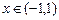 时,
时,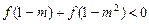 ,求实数
,求实数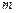 的取值集合;
的取值集合;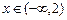 时,
时,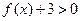 恒成立,求
恒成立,求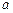 的取值范围.
的取值范围.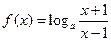 ,
,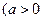 ,且
,且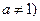

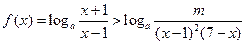 恒成立,求
恒成立,求 的取值范围;
的取值范围;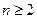 ,且
,且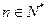 时,试比较
时,试比较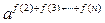 与
与 的大小.
的大小. 处时获悉,在其正东方向相距20海里的
处时获悉,在其正东方向相距20海里的 处有一艘渔船遇险
处有一艘渔船遇险 等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30
等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里
,相距10海里 处的乙船.
处的乙船.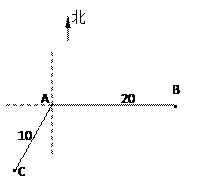
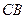 方向前往
方向前往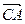 成
成 角,求
角,求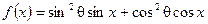
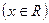 的值域.
的值域.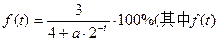 为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足
为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足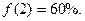
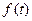 的表达式,计算
的表达式,计算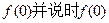 的含义;
的含义;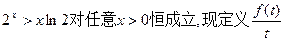 为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间
为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间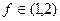 时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围。
时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围。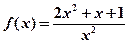 的值域为
的值域为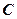 ,则( )
,则( )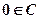 B
B .
.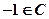 C.
C.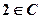 D.
D.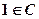

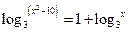 的解是 。
的解是 。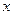 的方程
的方程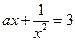 有且仅有一个正实数解,则实数
有且仅有一个正实数解,则实数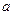 的取值范围是( )
的取值范围是( )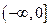
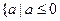 或
或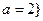
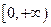
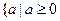 或
或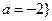
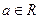 ,若函数
,若函数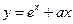 (
(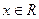 )的导函数有大于零的零点,则a的取值范围是___.
)的导函数有大于零的零点,则a的取值范围是___.