题目内容
(本小题满分14分)
已知函数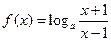 ,
,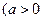 ,且
,且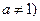
(Ⅰ)求函数的定义域,并证明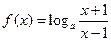 在定义域上是奇函数;
在定义域上是奇函数;
(Ⅱ)对于
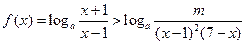 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅲ)当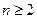 ,且
,且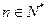 时,试比较
时,试比较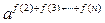 与
与 的大小.
的大小.
已知函数
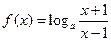 ,
,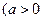 ,且
,且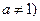
(Ⅰ)求函数的定义域,并证明
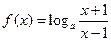 在定义域上是奇函数;
在定义域上是奇函数;(Ⅱ)对于

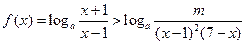 恒成立,求
恒成立,求 的取值范围;
的取值范围;(Ⅲ)当
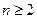 ,且
,且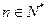 时,试比较
时,试比较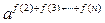 与
与 的大小.
的大小.(Ⅰ)函数的定义域为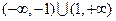 ,证明略
,证明略
(Ⅱ)①当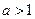 时,
时,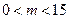 ;②当
;②当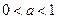 时,
时,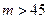
(Ⅲ)当 时,
时,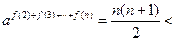

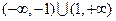 ,证明略
,证明略(Ⅱ)①当
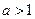 时,
时,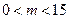 ;②当
;②当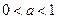 时,
时,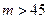
(Ⅲ)当
 时,
时,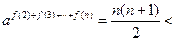

解:(Ⅰ)由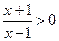 ,解得
,解得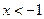 或
或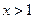 ,
,
∴ 函数的定义域为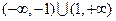 …………………2分
…………………2分
当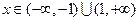 时,
时,
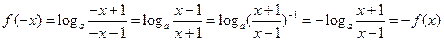
∴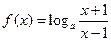 在定义域上是奇函数。 …………….4分
在定义域上是奇函数。 …………….4分
(Ⅱ)由 时,
时,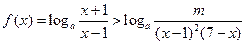 恒成立,
恒成立,
①当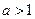 时
时
∴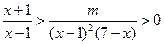 对
对 恒成立
恒成立
∴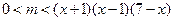 在
在 恒成立 ………………………6分
恒成立 ………………………6分
设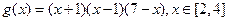
则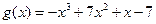
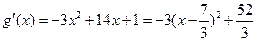
∴当 时,
时,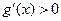
∴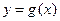 在区间
在区间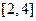 上是增函数,
上是增函数,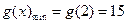
∴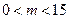 …………………………8分
…………………………8分
②当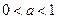 时
时
由 时,
时,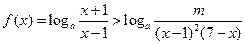 恒成立,
恒成立,
∴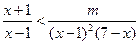 对
对 恒成立
恒成立
∴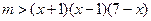 在
在 恒成立 ………………………9分
恒成立 ………………………9分
设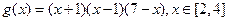
由①可知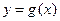 在区间
在区间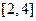 上是增函数,
上是增函数,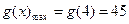
∴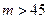 …………………………10分
…………………………10分
(Ⅲ)∵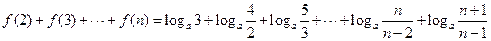
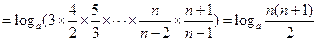
∴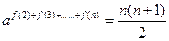
当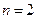 时,
时,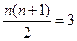 ,
, =2,∴
=2,∴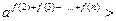

当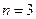 时,
时,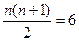 ,
, =6,∴
=6,∴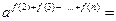

当 时,
时,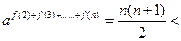
 …………………………12分
…………………………12分
下面证明:当 时,
时,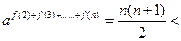

证法一:当 时,
时,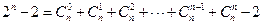
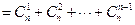
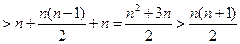
∴当 时,
时,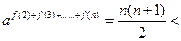
 …………………………14分
…………………………14分
证法二:当 时,要证明
时,要证明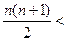

只需要证明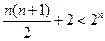
(1)当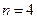 时,
时,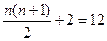 ,
,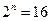 ,
,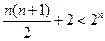 成立
成立
(2)假设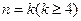 ,不等式
,不等式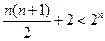 成立,即
成立,即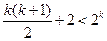
那么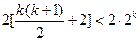
∴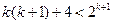
又因为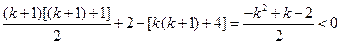
∴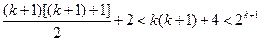
∴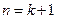 时,不等式
时,不等式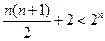 成立
成立
综合(1)和(2),对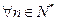 ,且
,且 不等式
不等式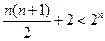 成立
成立
∴当 时,
时,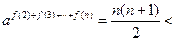
 …………………………14分
…………………………14分
证法三:∵ 时,
时,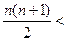

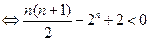
构造函数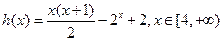
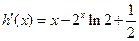
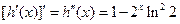
∴当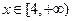 时,
时,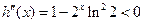
∴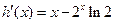 在区间
在区间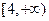 是减函数,
是减函数,
∴当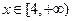 时,
时,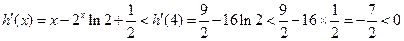
∴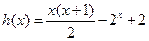 在区间
在区间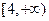 是减函数,
是减函数,
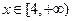 时,
时,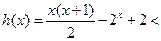

 时,
时,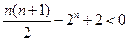 ,即
,即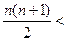

∴当 时,
时,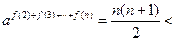
 …………………………14分
…………………………14分
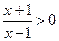 ,解得
,解得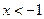 或
或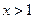 ,
,∴ 函数的定义域为
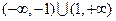 …………………2分
…………………2分当
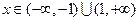 时,
时,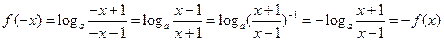
∴
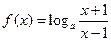 在定义域上是奇函数。 …………….4分
在定义域上是奇函数。 …………….4分(Ⅱ)由
 时,
时,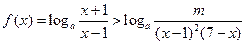 恒成立,
恒成立,①当
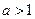 时
时∴
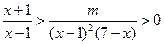 对
对 恒成立
恒成立∴
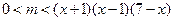 在
在 恒成立 ………………………6分
恒成立 ………………………6分设
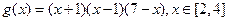
则
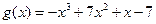
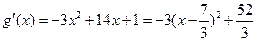
∴当
 时,
时,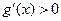
∴
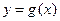 在区间
在区间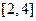 上是增函数,
上是增函数,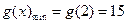
∴
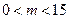 …………………………8分
…………………………8分②当
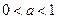 时
时由
 时,
时,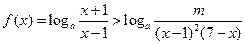 恒成立,
恒成立,∴
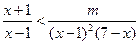 对
对 恒成立
恒成立∴
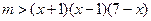 在
在 恒成立 ………………………9分
恒成立 ………………………9分设
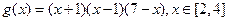
由①可知
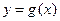 在区间
在区间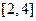 上是增函数,
上是增函数,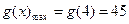
∴
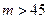 …………………………10分
…………………………10分(Ⅲ)∵
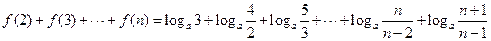
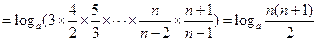
∴
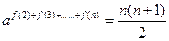
当
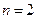 时,
时,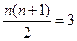 ,
, =2,∴
=2,∴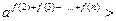

当
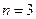 时,
时,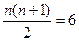 ,
, =6,∴
=6,∴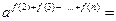

当
 时,
时,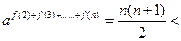
 …………………………12分
…………………………12分下面证明:当
 时,
时,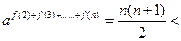

证法一:当
 时,
时,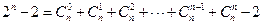
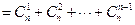
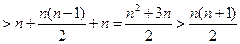
∴当
 时,
时,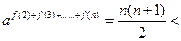
 …………………………14分
…………………………14分证法二:当
 时,要证明
时,要证明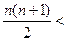

只需要证明
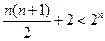
(1)当
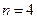 时,
时,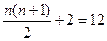 ,
,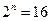 ,
,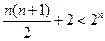 成立
成立(2)假设
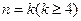 ,不等式
,不等式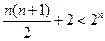 成立,即
成立,即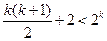
那么
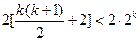
∴
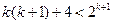
又因为
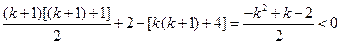
∴
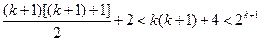
∴
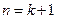 时,不等式
时,不等式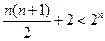 成立
成立综合(1)和(2),对
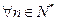 ,且
,且 不等式
不等式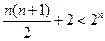 成立
成立∴当
 时,
时,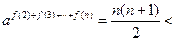
 …………………………14分
…………………………14分证法三:∵
 时,
时,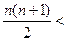

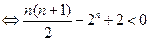
构造函数
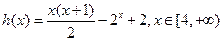
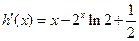
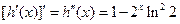
∴当
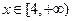 时,
时,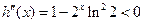
∴
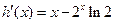 在区间
在区间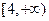 是减函数,
是减函数,∴当
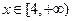 时,
时,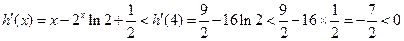
∴
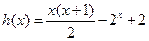 在区间
在区间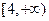 是减函数,
是减函数,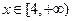 时,
时,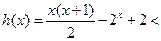

 时,
时,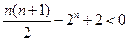 ,即
,即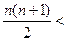

∴当
 时,
时,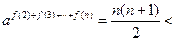
 …………………………14分
…………………………14分
练习册系列答案
相关题目
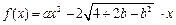 ,
,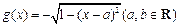 .
.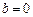 时,若
时,若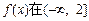 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;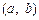 :存在
:存在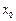 ,使得
,使得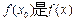 的最大值,
的最大值,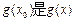 的最小值;
的最小值;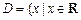 且
且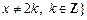 上的函数
上的函数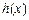 :使
:使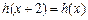 ,且当
,且当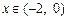 时,
时,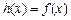 .
.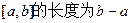 ,区间
,区间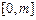 在映射
在映射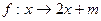 所得的对应区间为
所得的对应区间为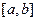 ,若区间
,若区间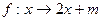 所得的对应区间为
所得的对应区间为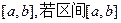 的长度比区间[0,m]的长度大5,则m= 。(定义区间
的长度比区间[0,m]的长度大5,则m= 。(定义区间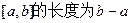 )
)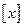 表示不超过实数
表示不超过实数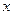 的最大整数,
的最大整数,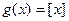 为取整函数,
为取整函数,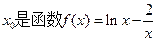 的零点,则
的零点,则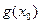 等于 ( )
等于 ( )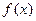 的图像恰好通过
的图像恰好通过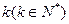 个格点,则称函数
个格点,则称函数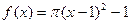 ②
②
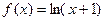 ④
④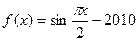

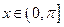 关于x的方程
关于x的方程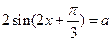 有两个不同的实数解,则实数a的取值范围为( )
有两个不同的实数解,则实数a的取值范围为( )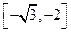 B
B 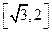 C
C 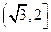 D
D 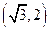
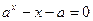 (a>0,a≠1)有两个不等实根,则a的取值范围是 ( )
(a>0,a≠1)有两个不等实根,则a的取值范围是 ( ) )
)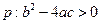 (
(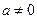 ),
),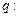 关于
关于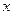 的方程
的方程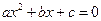 (
(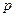 是
是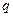 的( )
的( )