题目内容
【题目】如图放置的边长为2的正三角形
沿
轴滚动，记滚动过程中顶点
的横、纵坐标分别为和
，设是的函数，记
，则下列说法中：
①函数的图像关于轴对称；
②函数的值域是
；
③函数在
上是增函数；
④函数与
在
上有
个交点.
其中正确说法的序号是_______.
说明：“正三角形沿轴滚动”包括沿轴正方向和沿轴负方向滚动．沿轴正方向滚动指的是先以顶点B为中心顺时针旋转，当顶点C落在轴上时，再以顶点C为中心顺时针旋转，如此继续．类似地，正三角形可以沿轴负方向滚动．
【答案】①④
【解析】
根据说明在直角坐标系内，画出点
运动的轨迹.
根据图象可以直接判断出说法①②的正确性；
根据图象可以知道函数周期性，进而可以求出函数的增区间，从而可以判断出说法③的正确性；
先考虑当
，函数
与
的交点情况，根据函数的周期性，再求出函数与在
上交点的个数，从而判断出说法④的正确性，最后选出正确答案.
点运动的轨迹如图所示：
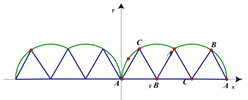
则函数图像关于
轴对称，故①正确；
的值域为
，故②不正确；
其增区间为
和
，故③正不确；
由图像可知，函数每6个单位一个循环，
当，函数与有3个交点，
∴当
，
，有
个交点，
有
个交点，
∴当
，有
个交点，
∴当
，有
个交点，故④正确．故选①④．
【题目】由国家公安部提出，国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准（
）》于
年
月
日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验，一般情况下，某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图，
喝瓶啤酒的情况
且图表示的函数模型
，则该人喝一瓶啤酒后至少经过多长时间才可以驾车（时间以整小时计算）？（参考数据：
，
）
（ ）
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值
A.
B.
C.D.
【题目】甲、乙两家外卖公司，其送餐员的日工资方案如下：甲公司的底薪70元，每单抽成4元；乙公司无底薪，40单以内（含40单）的部分每单抽成5元，超出40单的部分每单抽成7元，假设同一公司送餐员一天的送餐单数相同，现从两家公司各随机抽取一名送餐员，并分别记录其100天的送餐单数，得到如表频数表： 甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
（Ⅰ）现从甲公司记录的100天中随机抽取两天，求这两天送餐单数都大于40的概率；
（Ⅱ）若将频率视为概率，回答下列问题：
（i）记乙公司送餐员日工资为X（单位：元），求X的分布列和数学期望；
（ii）小明拟到甲、乙两家公司中的一家应聘送餐员，如果仅从日工资的角度考虑，请利用所学的统计学知识为他作出选择，并说明理由．
【题目】某商品要了解年广告费
（单位：万元）对年利润
（单位：万元）的影响，对近4年的年广告费
和年利润
数据作了初步整理，得到下面的表格：
广告费 | 2 | 3 | 4 | 5 |
年利润 | 26 | 39 | 49 | 54 |
（Ⅰ）用广告费作解释变量，年利润作预报变量，建立关于的回归直线方程；
（Ⅱ）根据（Ⅰ）的结果预报广告费用为6万元时的年利润.
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
.
