题目内容
【题目】已知函数![]() 的图象在
的图象在![]() 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为![]() 和
和![]() .若将函数
.若将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到的图象关于原点对称.
个单位长度后得到的图象关于原点对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 的周期为
的周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意可知函数![]() 的周期
的周期![]() ,且
,且![]() ,再结合函数图像的平移变换后图像关于原点对称,可得
,再结合函数图像的平移变换后图像关于原点对称,可得![]() ,结合
,结合![]() ,运算可得函数解析式;
,运算可得函数解析式;
(2)由(1)可得![]() ,令
,令![]() ,当
,当![]() 在
在![]() 上有两个不同的解,则
上有两个不同的解,则 ,又
,又![]() ,即可得实数
,即可得实数![]() 的范围.
的范围.
(1)由题意可知函数![]() 的周期
的周期![]() ,且
,且![]() ,所以
,所以![]() ,故
,故![]() .将函数
.将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到的图象对应的函数解析式为
个单位长度后得到的图象对应的函数解析式为![]() ,因为函数
,因为函数![]() 的图象关于原点对称,所以
的图象关于原点对称,所以![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() ,故
,故![]() .
.
(2)由(1)得函数![]() ,其周期为
,其周期为![]() ,
,
又![]() ,所以
,所以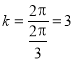 .令
.令![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
若![]() 在
在![]() 上有两个不同的解,则
上有两个不同的解,则 ,
,
所以当![]() 时,方程
时,方程![]() 在
在![]() 上恰有两个不同的解,即实数
上恰有两个不同的解,即实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某研究机构对高三学生的记忆力![]() 和判断力
和判断力![]() 进行统计分析,得下表数据:
进行统计分析,得下表数据:
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |

(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式: ,
,![]() .
.