题目内容
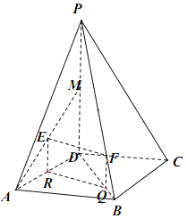
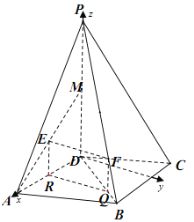
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 底面ABCD,且
底面ABCD,且![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析(2)![]()
【解析】
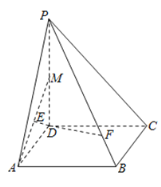
(1)(法一)如图,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,则有
,则有![]() ,利用线面平行的判定定理,证得
,利用线面平行的判定定理,证得![]() 平面
平面![]() ,进而证得
,进而证得![]() 平面
平面![]() ,从而证得平面
,从而证得平面![]() 平面
平面![]() ,即可求得
,即可求得![]() 平面
平面![]() .
.
(法二)连接![]() 、
、![]() 、
、![]() ,则有
,则有![]() ,证得
,证得![]() ,利用线面平行的判定定理,即可证得
,利用线面平行的判定定理,即可证得![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() ,求得平面
,求得平面![]() 和平面
和平面![]() 的一个法向量,利用向量的夹角公式,即可求解。
的一个法向量,利用向量的夹角公式,即可求解。
解:(1)证明:(法一)如图,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,则有
,则有![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() ,∴平面
,∴平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
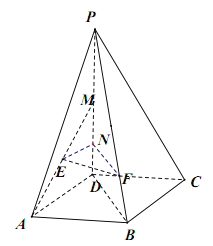
(法二)如图,设![]() 中点为
中点为![]() ,
,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.
连接![]() 、
、![]() 、
、![]() ,则有
,则有![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,且
,且![]() ,
,
即![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)∵平面![]() 底面
底面![]() ,且
,且![]() ,∴
,∴![]() 底面
底面![]() ,
,
如图,以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,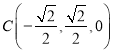 ,
,
∴![]() ,
,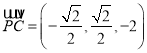 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则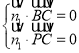 ,∴
,∴ ,
,
取![]() ,可得
,可得![]() ,
,
又易知平面![]() 的一个法向量
的一个法向量![]() ,
,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,则
,则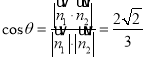 ,
,
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目