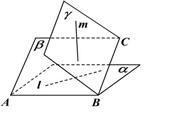
题目内容
如图,四棱锥 中,四边形
中,四边形 为矩形,
为矩形, 为等腰三角形,
为等腰三角形, ,平面
,平面 平面
平面 ,且
,且 ,
, 分别为
分别为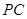 和
和 的中点.
的中点.

(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)证明:平面 平面
平面 ;
;
(Ⅲ)求四棱锥 的体积.
的体积.
 中,四边形
中,四边形 为矩形,
为矩形, 为等腰三角形,
为等腰三角形, ,平面
,平面 平面
平面 ,且
,且 ,
, 分别为
分别为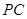 和
和 的中点.
的中点.
(Ⅰ)证明:
 平面
平面 ;
;(Ⅱ)证明:平面
 平面
平面 ;
;(Ⅲ)求四棱锥
 的体积.
的体积.(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)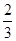 .
.
 .
.试题分析:(Ⅰ)证明线面平行,一般可考虑线面平行的判定定理,构造面外线平行于面内线,其手段一般是构造平行四边形,或构造三角形中位线(特别是有中点时),本题易证
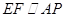 从而达到目标;(Ⅱ)要证面面垂直,由面面垂直的判定定理知可先考察线面垂直,要证线面垂直,又要先考察线线垂直;(Ⅲ)求棱锥的体积,关键是作出其高,由面
从而达到目标;(Ⅱ)要证面面垂直,由面面垂直的判定定理知可先考察线面垂直,要证线面垂直,又要先考察线线垂直;(Ⅲ)求棱锥的体积,关键是作出其高,由面 面
面 及
及 为等腰直角三角形,易知
为等腰直角三角形,易知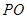 (
( 中点为
中点为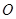 ),就是其高,问题得以解决.
),就是其高,问题得以解决.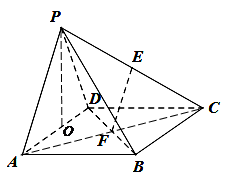
试题解析:(Ⅰ)证明:如图,连结
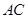 .
.∵四边形
 为矩形且
为矩形且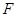 是
是 的中点.∴
的中点.∴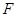 也是
也是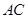 的中点.
的中点.又
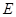 是
是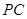 的中点,
的中点,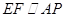 2分
2分∵
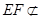 平面
平面 ,
,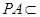 平面
平面 ,所以
,所以 平面
平面 ; 4分
; 4分(Ⅱ)证明:∵平面
 平面
平面 ,
,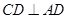 ,平面
,平面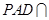 平面
平面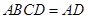 ,
,所以平面
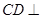 平面
平面 ,又
,又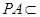 平面
平面 ,所以
,所以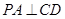 6分
6分又
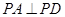 ,
,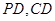 是相交直线,所以
是相交直线,所以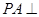 面
面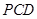
又
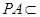 平面
平面 ,平面
,平面 平面
平面 ; 8分
; 8分(Ⅲ)取
 中点为
中点为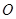 .连结
.连结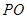 ,
, 为等腰直角三角形,所以
为等腰直角三角形,所以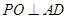 ,
,因为面
 面
面 且面
且面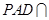 面
面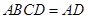 ,
,所以,
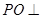 面
面 ,
,即
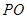 为四棱锥
为四棱锥 的高.
的高. 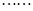 10分
10分 由
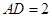 得
得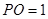 .又
.又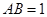 .
.∴四棱锥
 的体积
的体积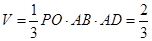 12分
12分
练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
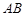 是圆的直径,
是圆的直径,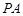 垂直于圆所在的平面,
垂直于圆所在的平面,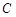 是圆上的点.
是圆上的点.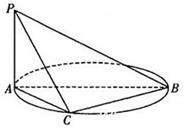
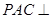 平面
平面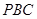 ;
;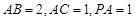 ,求二面角
,求二面角 的余弦值.
的余弦值. ,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
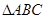 是边长为2的正三角形. 若
是边长为2的正三角形. 若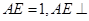 平面
平面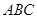 ,平面
,平面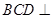 平面
平面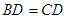 ,且
,且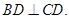
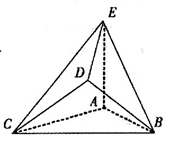
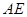 //平面
//平面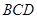 ;
; 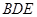
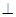 平面
平面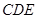 .
.  中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,若
上,若 ,则线段
,则线段 的长度等于______.
的长度等于______.
 且
且 .给出下列命题:
.给出下列命题: 且
且 ;
; 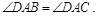
 、
、 、
、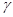 和直线
和直线 、
、 、
、 、
、 ,下列命题中真命题是 ( )
,下列命题中真命题是 ( ) ,则
,则 ;
; 则
则 ;
;  ,则
,则 ;
; ,则
,则 .
.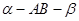 与
与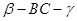 均为
均为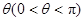 ,
,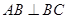 ,
,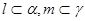 ,则下列不可能成立的是( )
,则下列不可能成立的是( )