题目内容
在如图所示的几何体中,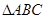 是边长为2的正三角形. 若
是边长为2的正三角形. 若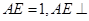 平面
平面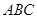 ,平面
,平面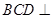 平面
平面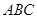 ,
, ,且
,且
(1)求证: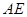 //平面
//平面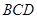 ;
;
(2)求证:平面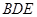
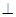 平面
平面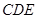 .
.
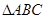 是边长为2的正三角形. 若
是边长为2的正三角形. 若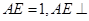 平面
平面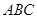 ,平面
,平面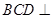 平面
平面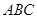 ,
,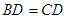 ,且
,且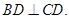

(1)求证:
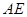 //平面
//平面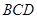 ;
; (2)求证:平面
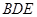
 平面
平面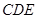 .
. (1)证明详见解析;(2)证明详见解析.
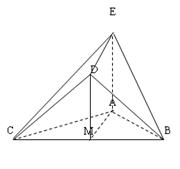
试题分析:(1)取
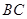 的中点
的中点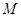 ,连接
,连接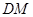 、
、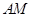 ,先根据已知条件证出
,先根据已知条件证出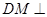 平面
平面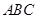 ,再证
,再证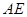 ∥
∥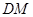 ,最后得出
,最后得出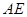 ∥平面
∥平面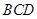 ;(2)先判断四边形
;(2)先判断四边形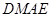 是平行四边形,利用已知证明
是平行四边形,利用已知证明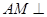 平面
平面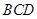 ,
,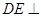 平面
平面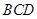 ,所以
,所以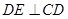 ,再证明
,再证明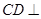 平面
平面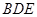 ,所以平面
,所以平面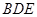 ⊥平面
⊥平面 .
.试题解析:
(1) 取
 的中点
的中点 ,连接
,连接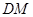 、
、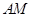 ,
,因为
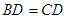 ,且
,且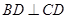 ,
,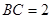
所以
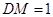 ,
,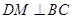 ,
,  . 1分
. 1分又因为平面
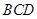 ⊥平面
⊥平面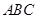 ,
, 所以
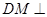 平面
平面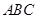 3分
3分因为
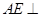 平面
平面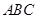 ,
, 所以
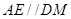 , 4分
, 4分又因为
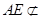 平面
平面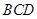 ,
,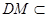 平面
平面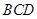 , 5分
, 5分所以
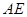 ∥平面
∥平面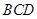 . 6分
. 6分(2)由(1)已证
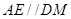 ,又
,又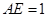 ,
,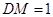 ,
, 所以四边形
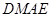 是平行四边形, 7分
是平行四边形, 7分所以
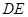 ∥
∥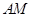 . 8分
. 8分由(1)已证
 ,又因为平面
,又因为平面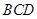 ⊥平面
⊥平面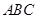 ,
, 所以
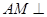 平面
平面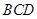 , 10分
, 10分所以
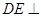 平面
平面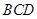 . 11分
. 11分又
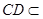 平面
平面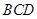 ,所以
,所以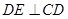 . 12分
. 12分因为
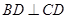 ,
,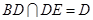 ,
,所以
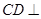 平面
平面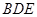 . 13分
. 13分因为
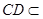 平面
平面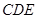 ,
, 所以平面
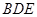 ⊥平面
⊥平面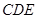 . 14分
. 14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,点
中,点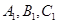 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且 ,E为
,E为 中点,
中点, .
.
 ,
, 平面
平面
 中,四边形
中,四边形 为矩形,
为矩形, 为等腰三角形,
为等腰三角形, ,平面
,平面 平面
平面 ,
, 分别为
分别为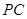 和
和 的中点.
的中点.
 平面
平面 ;
; 平面
平面 中,点
中,点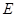 是
是 的中点,点
的中点,点 是
是 的中点,将△
的中点,将△ 、△
、△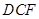 分别沿
分别沿 、
、 折起,使
折起,使 、
、 两点重合于点
两点重合于点 ,连接
,连接 ,
, .
.

 ; (2)求点
; (2)求点 的距离.
的距离. 的底面为矩形,
的底面为矩形, ,
, ,
, 分别是
分别是 的中点,
的中点, .
.
 平面
平面 ;
; 平面
平面 .
. 中,侧棱
中,侧棱 底面
底面 ,
,

 平面
平面
 与平面
与平面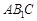 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值 ,写出
,写出 、
、 和平面
和平面 ,若
,若 ,则“
,则“ ”是“
”是“ ”的( )
”的( )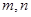 和不重合的平面
和不重合的平面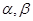 ,下列命题错误的是( )
,下列命题错误的是( ) ,则
,则
 ,则
,则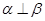
 ,则
,则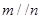
 ,则
,则