题目内容
如图所示,在圆锥PO中, PO= ,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
,?O的直径AB=2, C为弧AB的中点,D为AC的中点.

(1)求证:平面POD^平面PAC;
(2)求二面角B—PA—C的余弦值.
 ,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
(1)求证:平面POD^平面PAC;
(2)求二面角B—PA—C的余弦值.
(1)见解析;(2)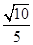
试题分析:(1)通过证平面PAC内直线AC^平面POD,由平面与平面垂直的判定定理得平面PAC^平面POD;(2)用垂面法作出二面角的平面角,然后在直角三角形中利用边长求平面角的余弦值.
试题解析:证明:(1)如图所示,连接OC.
 OA=OC,D是AC的中点,\AC^OD,在圆锥PO中,PA=PC,
OA=OC,D是AC的中点,\AC^OD,在圆锥PO中,PA=PC,则AC^PD,又PDÇOD=D,\AC^平面POD,而ACÌ平面PAC,
\平面POD^平面PAC 5分
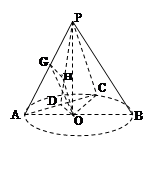
(2)在平面POD中,过O作OH^PD于H,由(1)知:
平面POD^平面PAC,\OH^平面PAC,过H作HG^PA于G,连OG,则OG^PA(三垂线定理)
\ÐOGH为二面角B—PA—C的平面角,
在RtDODA中,OD=OA×450=
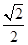 .
.在RtDPOD中,OH=
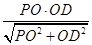 =
= 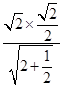 =
=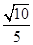 .
.在RtDPOA中,OG=
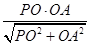 =
= 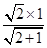 =
=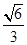 .
.在RtDOHG中,sinÐOGH=
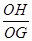 =
= 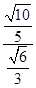 =
=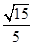 .
.所以,cosÐOGH=
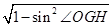 =
= 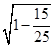 =
=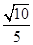
所以,二面角B—PA—C的余弦值为
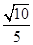 . 10分
. 10分
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 中,
中, ⊥底面
⊥底面 ,
,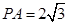 ,
, ,
,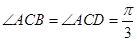 .
.
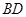 ⊥平面
⊥平面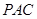 ;
; 上的点
上的点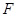 满足
满足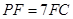 ,求三棱锥
,求三棱锥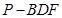 的体积.
的体积. 中,四边形
中,四边形 为矩形,
为矩形, 为等腰三角形,
为等腰三角形, ,平面
,平面 平面
平面 ,
, 分别为
分别为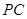 和
和 的中点.
的中点.
 平面
平面 ;
; 平面
平面 的底面为矩形,
的底面为矩形, ,
, ,
, 分别是
分别是 的中点,
的中点, .
.
 平面
平面 ;
; 平面
平面 .
.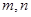 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,下列四个命题中假命题的是( )
是三个不同的平面,下列四个命题中假命题的是( ) 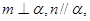 则
则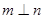
 则
则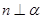
 则
则
 ,则
,则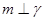
 //平面
//平面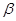 ,
,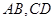 是夹在
是夹在 间的线段,若
间的线段,若 //
//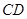 ,则
,则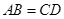 ;
; 是异面直线,
是异面直线,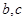 是异面直线,则
是异面直线,则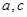 一定是异面直线;
一定是异面直线;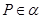 ,
, //
//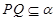 ;
; 、
、 是不同的直线,
是不同的直线, 、
、 是不同的平面,则下列命题:
是不同的平面,则下列命题: ,则
,则 ;②若
;②若 ,则
,则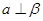 ;
; ,则
,则 ;④若
;④若 ,则
,则 .
.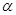 、
、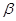 表示不同的平面,
表示不同的平面,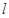 、
、 、
、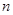 表示不同直线,则以下命题中正确的有 ( )
表示不同直线,则以下命题中正确的有 ( )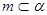 ,
,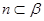 ,则
,则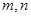 是两条不同的直线,
是两条不同的直线,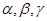 是三个不同的平面,下列命题中错误的是( )
是三个不同的平面,下列命题中错误的是( )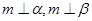 ,则
,则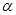 ∥
∥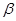
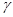 ,
,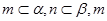 ∥
∥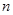 ,则
,则