题目内容
已知矩阵A的逆矩阵A－1＝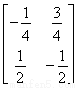
，求矩阵A的特征值．
λ1＝－1，λ2＝4
【解析】
解 因为A－1A＝E，所以A＝(A－1)－1.
因为A－1＝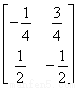
，所以A＝(A－1)－1＝
，
于是矩阵A的特征多项式为f(λ)＝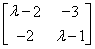
＝λ2－3λ－4.
令f(λ)＝0，解得A的特征值λ1＝－1，λ2＝4.
练习册系列答案
阅读快车系列答案
相关题目
题目内容
已知矩阵A的逆矩阵A－1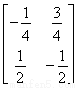＝，求矩阵A的特征值．
λ1＝－1，λ2＝4
【解析】
解 因为A－1A＝E，所以A＝(A－1)－1.
因为A－1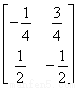＝，所以A＝(A－1)－1＝，
于是矩阵A的特征多项式为f(λ)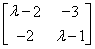＝＝λ2－3λ－4.
令f(λ)＝0，解得A的特征值λ1＝－1，λ2＝4.
阅读快车系列答案
