题目内容
【题目】已知正方形ABCD的边长为4,M是AD的中点,动点N在正方形ABCD的内部或其边界移动,并且满足![]() ,则
,则![]() 的取值范围是________.
的取值范围是________.
【答案】![]()
【解析】
以A为原点建立直角坐标系,可得A(0,0),B(4,0),C(4,4),D(0,4),M(0,2),可得N满足的方程![]() (x≥0),同时可得
(x≥0),同时可得![]() =
=![]() ,设z=
,设z=![]() ,求出其取值范围可得答案.
,求出其取值范围可得答案.
解: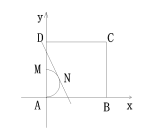
如图以A为原点建立直角坐标系,可得A(0,0),B(4,0),C(4,4),D(0,4),M(0,2)
设N点坐标N(x,y),可得![]() =(x,y-2),
=(x,y-2),![]() =(x,y),由
=(x,y),由![]() ,可得N满足的方程
,可得N满足的方程![]() (x≥0)…①,可得
(x≥0)…①,可得![]() =(4-x,-y),
=(4-x,-y),![]() =(4-x,4-y),可得
=(4-x,4-y),可得![]() =
=![]() =
=![]() …②,将①代入②可得
…②,将①代入②可得![]() =
=![]() ,
,
即求z=![]() 的取值范围,
的取值范围,
可得(x,y)满足![]() (x≥0),由图像可知当N取(0,0)点的时候z最大,
(x≥0),由图像可知当N取(0,0)点的时候z最大,![]() ,当直线z=
,当直线z=![]() 与圆
与圆![]() (x≥0)相切时候,z取最小值,
(x≥0)相切时候,z取最小值,
设直线为y=-2x+b,则z=-2b+16,
联立方程可得![]() ,可得
,可得![]() ,由其只有一个交点可得:
,由其只有一个交点可得:
△=0,即:![]() ,解得:b=
,解得:b=![]() 或b=
或b=![]() (b>0,舍去),
(b>0,舍去),
![]() z=-2b+16=14-2
z=-2b+16=14-2![]() ,即:
,即:![]() ,
,
可得![]() 的取值范围:
的取值范围:![]() .
.

【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
【题目】通过随机询问![]() 名不同性别的大学生是否爱好某项运动,得到如下的
名不同性别的大学生是否爱好某项运动,得到如下的![]() 列联表:
列联表:
男 | 女 | |
爱好 | 40 | 20 |
不爱好 | 20 | 30 |
由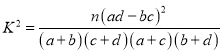 算得
算得![]() ,
,
参照附表,以下不正确的有( )
附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.在犯错误的概率不超过![]() 的前提下,认为“爱好该项运动与性别有关”
的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过![]() 的前提下,认为“爱好该项运动与性别无关”
的前提下,认为“爱好该项运动与性别无关”
C.有![]() 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”
D.有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”


