题目内容
(本题满分16分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分6分.
(文)已知椭圆 的一个焦点为
的一个焦点为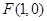 ,点
,点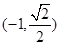 在椭圆
在椭圆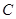 上,点
上,点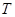 满足
满足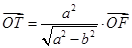 (其中
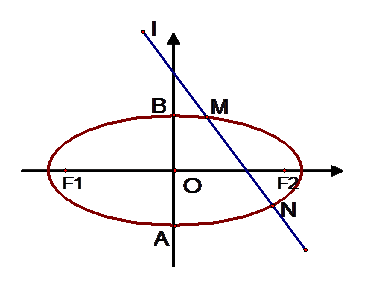
(其中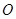 为坐标原点), 过点
为坐标原点), 过点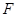 作一斜率为
作一斜率为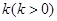 的直线交椭圆于
的直线交椭圆于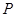 、
、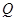 两点(其中
两点(其中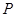 点在
点在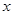 轴上方,
轴上方,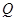 点在
点在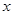 轴下方) .
轴下方) .
(1)求椭圆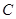 的方程;
的方程;
(2)若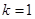 ,求
,求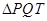 的面积;
的面积;
(3)设点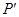 为点
为点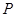 关于
关于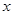 轴的对称点,判断
轴的对称点,判断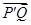 与
与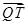 的位置关系,并说明理由.
的位置关系,并说明理由.
(1)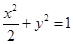 (2)
(2)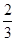 (3)
(3)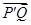 与
与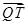 共线,设出点的坐标,用向量的坐标运算即可证明.
共线,设出点的坐标,用向量的坐标运算即可证明.
解析试题分析:(1)由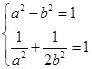 ,得 ……2分
,得 ……2分
解得a2=2,b2=1,
所以,椭圆方程为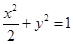 . ……4分
. ……4分
(2)设PQ:y=x-1,
由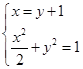 得3y2+2y-1=0, ……6分
得3y2+2y-1=0, ……6分
解得: P(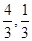 ),Q(0,-1),
),Q(0,-1),
由条件可知点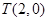 ,
,
所以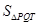 =
=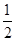 |FT||y1-y2|=
|FT||y1-y2|=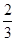 . ……10分
. ……10分
(3) 判断: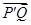 与
与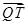 共线. ……11分
共线. ……11分
设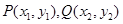
则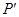 (x1,-y1),
(x1,-y1),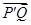 =(x2-x1,y2+y1),
=(x2-x1,y2+y1),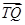 =(x2-2,y2), ……12分
=(x2-2,y2), ……12分
由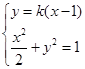 得
得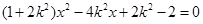 . ……13分
. ……13分
(x2-x1)y2-(x2-2)(y1+y2)=(x2-x1)k(x2-1)-(x2-2)(kx1-k+kx2-k)
=3k(x1+x2)-2kx1x2-4k=3k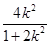 -2k
-2k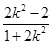 -4k
-4k
=k(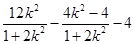 )=0. ……15分
)=0. ……15分
所以,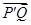 与
与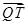 共线. ……16分
共线. ……16分
考点:本小题主要考查椭圆标准方程的求解、直线与椭圆的位置关系的判定和应用以及向量共线的坐标运算的应用,考查学生的运算求解能力和思维的严密性.
点评:高考中圆锥曲线的题目一般难度较大,而且一般运算量较大,要仔细运算,更要结合图形数形结合简化求解过程.

 新思维寒假作业系列答案
新思维寒假作业系列答案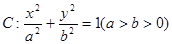 的离心率为
的离心率为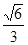 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
,椭圆C上任意一点到椭圆两个焦点的距离之和为6。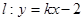 与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线
与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线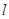 的方程。
的方程。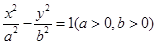 的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为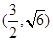 .
.
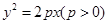 ,过其焦点F的直线交抛物线于
,过其焦点F的直线交抛物线于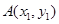 、
、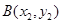 两点。过
两点。过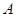 、
、 作准线的垂线,垂足分别为
作准线的垂线,垂足分别为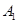 、
、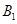 .
.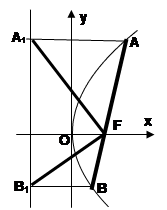
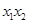 和
和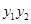 都是定值,并求出这个定值;
都是定值,并求出这个定值;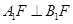 .
.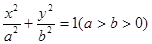 的离心率
的离心率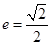 ,左焦点为
,左焦点为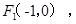 右焦点为
右焦点为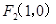 ,短轴两个端点为
,短轴两个端点为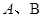 .与
.与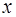 轴不垂直的直线
轴不垂直的直线 与椭圆C交于不同的两点
与椭圆C交于不同的两点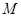 、
、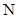 ,记直线
,记直线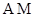 、
、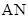 的斜率分别为
的斜率分别为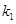 、
、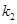 ,且
,且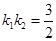 .
.
 的方程;
的方程;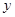 轴相交于定点,并求出定点坐标.
轴相交于定点,并求出定点坐标. 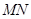 的中点
的中点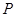 落在
落在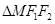 内(包括边界)时,求直线
内(包括边界)时,求直线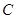 :
: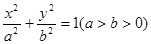 ,称圆心在原点
,称圆心在原点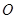 ,半径为
,半径为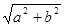 的圆是椭圆
的圆是椭圆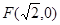 ,其短轴上的一个端点到
,其短轴上的一个端点到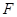 的距离为
的距离为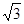 .
. 是椭圆
是椭圆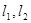 使得
使得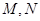 ,求证:
,求证: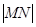 为定值.
为定值.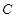 是动点
是动点 到两个定点
到两个定点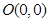 、
、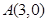 距离之比为
距离之比为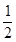 的点的轨迹。
的点的轨迹。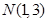 与曲线
与曲线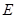 的对称轴为坐标轴,焦点在
的对称轴为坐标轴,焦点在 轴上,离心率
轴上,离心率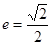 ,
,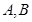 分别为椭圆的上顶点和右顶点,且
分别为椭圆的上顶点和右顶点,且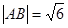 .
.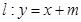 与椭圆
与椭圆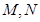 两点,且
两点,且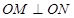 (其中
(其中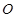 为坐标原点),求
为坐标原点),求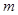 的值.
的值. 的离心率为
的离心率为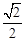 ,其中左焦点
,其中左焦点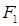 (-2,0).
(-2,0).