题目内容
(本题满分12分)
已知椭圆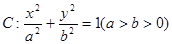 的离心率为
的离心率为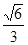 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
(1)求椭圆C的方程;
(2)设直线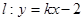 与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线
与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线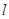 的方程。
的方程。
(1)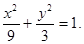 (2)
(2)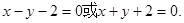
解析试题分析:解:(I)由已知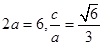 ,解得
,解得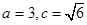
所以椭圆C的方程为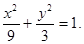
(2)由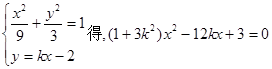 ,
,
直线与椭圆有两个不同的交点,所以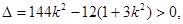
解得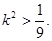
设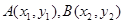 ,
,
则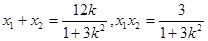
计算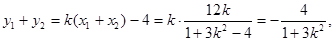
所以,A,B中点坐标为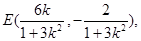
因为|PA|=|PB|,所以PE⊥AB,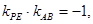
所以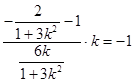 ,解得
,解得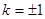 ,经检验,符合题意,
,经检验,符合题意,
所以直线l的方程为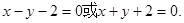
考点:椭圆的标准方程;两直线垂直的条件。
点评:当一道题出现什么样的曲线时,它有什么特点要先明确,一般在解题过程中都可能用到,像本题第一小题用到椭圆的特点:椭圆上任何一点到两焦点的距离之和等于2a。第二题关键要转换|PA|=|PB|为PE⊥AB(E为A、B的中点)。

练习册系列答案
相关题目
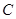 :
: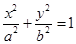 (
(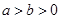 )的离心率为
)的离心率为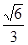 ,过右焦点
,过右焦点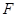 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆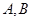 两点,
两点,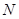 为弦
为弦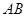 的中点。
的中点。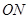 (
( 为坐标原点)的斜率
为坐标原点)的斜率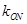 ;
;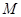 椭圆
椭圆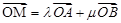 ,求
,求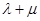 的最大值和最小值.
的最大值和最小值. 与椭圆
与椭圆 相交于
相交于 两个不同的点,与
两个不同的点,与 轴相交于点
轴相交于点 ,记
,记 为坐标原点.
为坐标原点.
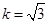 且
且 的面积及椭圆方程.
的面积及椭圆方程.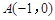 ,
,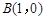 ,△
,△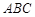 的周长为6.
的周长为6. 的轨迹
的轨迹 的方程;
的方程;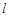 与曲线
与曲线 ,
,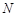 .若点
.若点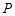 在
在 轴上,且
轴上,且 ,求点
,求点 与直线
与直线 相交于
相交于 两点,且
两点,且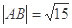
 的值。
的值。 上是否存在点
上是否存在点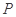 ,使得
,使得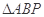 的重心恰为抛物线
的重心恰为抛物线 ,若存在,求点
,若存在,求点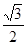 。
。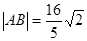 ,求直线l的方程。
,求直线l的方程。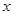 轴上的椭圆
轴上的椭圆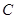 过点
过点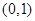 ,且离心率为
,且离心率为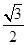 ,
,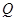 为椭圆
为椭圆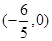 的直线
的直线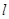 与椭圆
与椭圆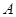 ,
,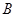 两点.
两点.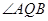 的大小;
的大小;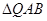 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线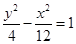 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为 ,若椭圆的焦点在
,若椭圆的焦点在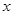 轴上,求椭圆的方程.
轴上,求椭圆的方程. 的一个焦点为
的一个焦点为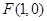 ,点
,点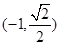 在椭圆
在椭圆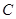 上,点
上,点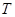 满足
满足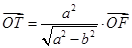 (其中
(其中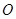 为坐标原点), 过点
为坐标原点), 过点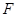 作一斜率为
作一斜率为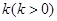 的直线交椭圆于
的直线交椭圆于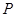 、
、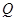 两点(其中
两点(其中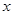 轴上方,
轴上方,
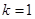 ,求
,求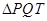 的面积;
的面积;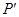 为点
为点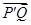 与
与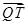 的位置关系,并说明理由.
的位置关系,并说明理由.