题目内容
(本题满分12分)给定椭圆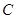 :
: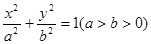 ,称圆心在原点
,称圆心在原点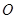 ,半径为
,半径为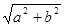 的圆是椭圆
的圆是椭圆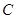 的“准圆”。若椭圆
的“准圆”。若椭圆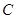 的一个焦点为
的一个焦点为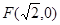 ,其短轴上的一个端点到
,其短轴上的一个端点到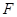 的距离为
的距离为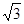 .
.
(Ⅰ)求椭圆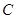 的方程和其“准圆”方程.
的方程和其“准圆”方程.
(Ⅱ)点 是椭圆
是椭圆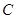 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点 作直线
作直线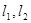 使得
使得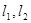 与椭圆
与椭圆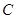 都只有一个交点,且
都只有一个交点,且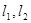 分别交其“准圆”于点
分别交其“准圆”于点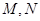 ,求证:
,求证: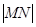 为定值.
为定值.
(Ⅰ)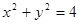
(Ⅱ)根据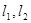 斜率情况进行分类讨论,分别证明知直线
斜率情况进行分类讨论,分别证明知直线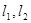 垂直,从而
垂直,从而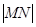 =4
=4
解析

练习册系列答案
相关题目
题目内容
(本题满分12分)给定椭圆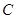 :
: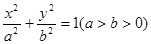 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为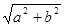 的圆是椭圆
的圆是椭圆 的“准圆”。若椭圆
的“准圆”。若椭圆 的一个焦点为
的一个焦点为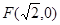 ,其短轴上的一个端点到
,其短轴上的一个端点到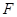 的距离为
的距离为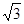 .
.
(Ⅰ)求椭圆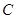 的方程和其“准圆”方程.
的方程和其“准圆”方程.
(Ⅱ)点 是椭圆
是椭圆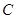 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点 作直线
作直线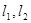 使得
使得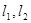 与椭圆
与椭圆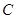 都只有一个交点,且
都只有一个交点,且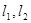 分别交其“准圆”于点
分别交其“准圆”于点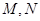 ,求证:
,求证: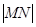 为定值.
为定值.
(Ⅰ)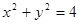
(Ⅱ)根据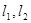 斜率情况进行分类讨论,分别证明知直线
斜率情况进行分类讨论,分别证明知直线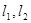 垂直,从而
垂直,从而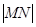 =4
=4
解析
