题目内容
已知抛物线的顶点在原点,它的准线过双曲线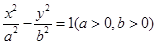 的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为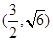 .
.
(1)求抛物线的方程;
(2)求双曲线的方程.
(1)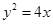 ;(2)
;(2)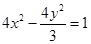
解析试题分析:(1)由题意知,抛物线的焦点在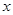 轴上,又过点
轴上,又过点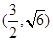 ,
,
所以,设抛物线方程为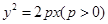 , 2分
, 2分
代入点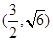 ,有
,有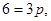
得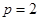 , 5分
, 5分
所以抛物线的方程为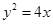 6分
6分
(2)由(1)知所求双曲线的一个焦点为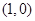 ,
,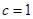 9分
9分
设所求双曲线方程为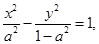 代入点
代入点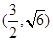 ,得
,得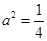 ,
,
故所求双曲线的方程为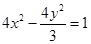 12分
12分
考点:本题考查了抛物线与双曲线方程的求法
点评:求指定的圆锥曲线的方程是高考命题的重点,主要考查识画图、数形结合、等价转化、分类讨论、逻辑推理、合理运算及创新思维能力,解决好这类问题,除要求熟练掌握好圆锥曲线的定义、性质外,命题人还常常将它与对称问题、弦长问题、最值问题等综合在一起命制难度较大的题

练习册系列答案
相关题目
 与椭圆
与椭圆 相交于
相交于 两个不同的点,与
两个不同的点,与 轴相交于点
轴相交于点 ,记
,记 为坐标原点.
为坐标原点.
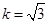 且
且 的面积及椭圆方程.
的面积及椭圆方程.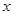 轴上的椭圆
轴上的椭圆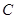 过点
过点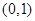 ,且离心率为
,且离心率为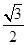 ,
,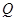 为椭圆
为椭圆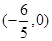 的直线
的直线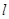 与椭圆
与椭圆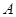 ,
,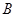 两点.
两点.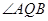 的大小;
的大小;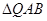 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线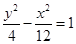 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为 ,若椭圆的焦点在
,若椭圆的焦点在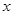 轴上,求椭圆的方程.
轴上,求椭圆的方程.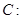
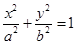 (
(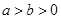 )的一个顶点为
)的一个顶点为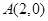 ,离心率为
,离心率为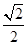 ,直线
,直线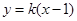 与椭圆
与椭圆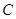 交于不同的两点
交于不同的两点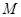 、
、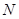 .(1) 求椭圆
.(1) 求椭圆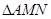 的面积为
的面积为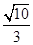 时,求
时,求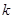 的值.
的值.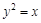 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|=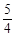 .
. 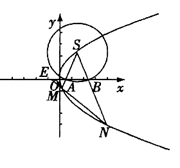
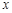 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;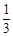 |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值. ,离心率
,离心率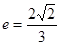 。
。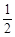 ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。 的一个焦点为
的一个焦点为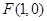 ,点
,点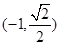 在椭圆
在椭圆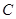 上,点
上,点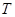 满足
满足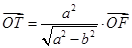 (其中
(其中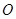 为坐标原点), 过点
为坐标原点), 过点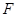 作一斜率为
作一斜率为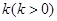 的直线交椭圆于
的直线交椭圆于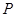 、
、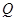 两点(其中
两点(其中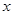 轴上方,
轴上方,
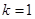 ,求
,求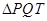 的面积;
的面积;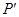 为点
为点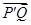 与
与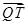 的位置关系,并说明理由.
的位置关系,并说明理由.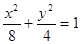 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为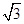 .
.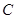 的方程;
的方程;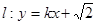 与双曲线
与双曲线 和
和 ,且
,且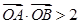
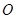 为原点),求
为原点),求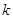 的取值范围.
的取值范围.