题目内容
15.设f(x)是定义在R上的减函数,且对任意实数x,y都有f(x+y)=f(x)+f(y).(1)求f(0)的值;
(2)求证f(x)是奇函数;
(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
分析 (1)令x=y=0,计算即可得到f(0);(2)可令x+y=0,结合(1)的结论,由奇偶性的定义,即可得证;
(3)运用(2)的结论和条件:f(x)是定义在R上的减函数,可得不等式t2-2t>k-2t2,再由参数分离和二次函数的最值求法,即可得到所求范围.
解答 解:(1)对任意实数x,y都有f(x+y)=f(x)+f(y),
可令x=y=0,可得f(0)=2f(0),
解得f(0)=0;
(2)证明:令x+y=0,即y=-x,
则f(0)=f(x)+f(-x),
由f(0)=0,可得f(-x)=-f(x),
则f(x)为奇函数;
(3)解:对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,
即有f(t2-2t)<-f(2t2-k),
由f(-x)=-f(x),可得
f(t2-2t)<f(-2t2+k),
由f(x)是定义在R上的减函数,
即有t2-2t>k-2t2,
即k<3t2-2t恒成立,
由3t2-2t=3(t-$\frac{1}{3}$)2-$\frac{1}{3}$,可得t=$\frac{1}{3}$,
取得最小值-$\frac{1}{3}$,
则k<-$\frac{1}{3}$.
故k的取值范围是(-∞,-$\frac{1}{3}$).
点评 本题考查函数的单调性和奇偶性的运用:解不等式,考查赋值法的运用,以及运算求解能力,属于中档题.

练习册系列答案
相关题目
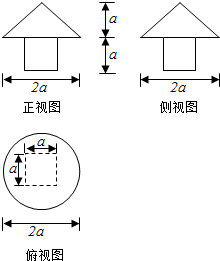 一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.
一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.