题目内容
【题目】给定一个
项的实数列
， 
， 
， 
，任意选取一个实数
，变换
将数列
， 
， 
， 
变换为数列
， 
， 
， 
，再将得到的数列继续实施这样的变换，这样的变换可以连续进行多次，并且每次所选择的实数
可以不相同，第
次变换记为
，其中
为第
次变换时所选择的实数．如果通过
次变换后，数列中的各项均为
，则称
， 
， 
， 
为“
次归零变换”．
（
）对数列
， 
， 
， 
，给出一个“
次归零变换”，其中
．
（
）对数列
， 
， 
， 
， 
，给出一个“
次归零变换”，其中
．
（
）证明：对任意
项的实数列，都存在“
次归零变换”．
【答案】（1）见解析；（2）见解析；（3）见解析
【解析】试题分析：（1）根据新定义，计算经变换
； 
； 
； 
，可得结论；（2）计算经变换
， 
， 
， 
， 
可得结论；（3）记经过
变换后，数列为
， 
， 
，取
， 
，继续做类似的变换，取
，（ 
，经
后，得到数列的前
项相等，再取
，经
后，即可得到结论；
试题解析：（
）
： 
， 
， 
， 
； 
： 
， 
， 
， 
； 
： 
， 
， 
， 
； 
： 
， 
， 
， 
．
（
）
： 
， 
， 
， 
， 
； 
： 
， 
， 
， 
， 
； 
： 
， 
， 
， 
， 
； 
： 
， 
， 
， 
， 
； 
： 
， 
， 
， 
， 
．
（
）证明：经过
次变换后，数列记为
， 
， 
， 
， 
， 
，
取
，则
，即经
后，前两项相等；
取
，则
，
即经
后，前三项相等； 
设进行变换
时， 
，变换后数列变为
， 
， 
， 
， 
，则
；
那么，进行第
次变换时，取
，
则变换后数列变为： 
， 
， 
， 
， 
， 
， 
， 
，
显然有
； 
经过
次变换后，显然有
；
最后，取
，经过变换
后，数列各项均为
，
所以对任意数列，都存在“
次归零变换”．
【题目】为了解某校学生参加社区服务的情况，采用按性别分层抽样的方法进行调查.已知该校共有学生960人，其中男生560人，从全校学生中抽取了容量为
的样本，得到一周参加社区服务的时间的统计数据好下表：
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
（Ⅰ）求
，；
（Ⅱ）能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关？
（Ⅲ）以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率，现从该校学生中随机调查6名学生，试估计6名学生中一周参加社区服务时间超过1小时的人数.
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y（万元）的几组对照数据:
x（年） | 2 | 3 | 4 | 5 | 6 |
y（万元） | 1 | 2.5 | 3 | 4 | 4.5 |
（1）若知道y对x呈线性相关关系，请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低?参考公式: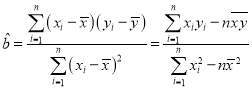
，
.