题目内容
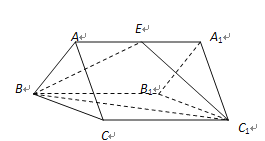
【题目】如图:三棱柱![]() 的所有棱长均相等,
的所有棱长均相等,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)连接CB1交BC1于点O,利用等腰三角形的三线合一证明线线垂直,再利用线面垂直的判定定理和面面垂直的判定定理进行证明;(2)取A1B1的中点
为H,连接C1H、BH,利用面面垂直的判定定理和性质定理得到线面垂直,即作出线面角,再利用直角三角形进行求解.
试题解析:(1)
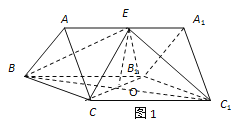
如图1,连接CB1交BC1于点O,则O为CB1与BC1的中点,连接EC,EB1 依题意有EB=EC1=EC=EB1
∴EO⊥CB1,EO⊥BC1, ∴EO⊥平面BCC1B1,![]()
∴平面EBC1⊥平面BCC1B1,
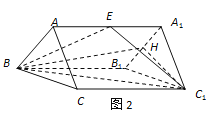
(2)如图2取A1B1的中点为H,连接C1H、BH,
∵![]() ,∴平面A1B1C1⊥平面BB1A1A,
,∴平面A1B1C1⊥平面BB1A1A,
平面A1B1C1![]() 平面BB1A1A= A1B1,
平面BB1A1A= A1B1,
又∵A1C1=B1C1,H为A1B1的中点,∴C1H⊥A1B1,∴C1H⊥平面BB1A1A,
则∠C1BH为直线BC1与平面BB1A1A所成的角。
令棱长为2a,则C1H=![]() ,BC1=
,BC1=![]() ,
,
∴![]()
所以直线BC1与平面BB1A1A所成角的正弦值为![]()

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)判断是否有![]() 的把握认为学生的学习积极性与对待班级工作的态度有关系?
的把握认为学生的学习积极性与对待班级工作的态度有关系?
附:  , n=a+b+c+d.
, n=a+b+c+d.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数x/个 | 2 | 3 | 4 | 5 |
加工的时间y/h | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
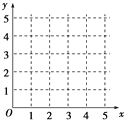
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间.